如图所示,B端悬挂一重为G的重物,不计杠杆自重,在A点施加动力F使杠杆保持水平平衡.则下列说法正确的是
| A.因为OA大于OB,所以F小于G |
| B.当杠杆平衡时,一定满足G×OB=F×OA |
| C.因为B点受到的拉力是向下的,所以F的方向一定向上 |
| D.F的大小可能大于G |
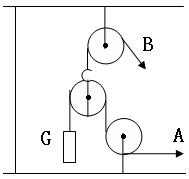
某人到健身房进行健身运动,用如图所示的牵引装置来锻炼腿部和手臂的力量。使用时:(1)绳子固定在A处,用手在B处用力FB拉绳子,使重物G匀速上升;(2)绳子固定在B处,用腿在A处用力FA拉绳子,使重物G匀速上升。以下结论正确的是(不考虑滑轮重和摩擦)( )
| A.FA>FB | B.FA<FB | C.FA="FB" | D.条件不足,无法确定 |
.下列估计值合理的是( )
| A.长跑运动员的体温可达46℃ |
| B.短跑运动员的速度可达72 km/h |
| C.足球运动员的质量可达80 kg |
| D.举重运动员的举力可达5000 N |
小明同学利用活塞式抽水机吸水时,忽然想到用活塞抽水机吸水时所用压力与大气压和水的深度有关。他灵机一动,想测算一下地下水的深度,他找来刻度尺测出相关数据,(如图)并把一个空水桶用绳系在压柄末端,并使压柄处于水平位置,逐渐向桶内加水,当压柄开始匀速下落时取下,用杆称出桶与水总质量为7.85kg.如果当时大气压为1标准大气压。活塞与筒壁摩擦不计g=10N/kg,试计算地下水距地面的深度为多少米?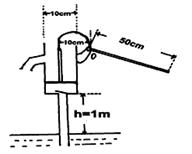
下图是一个上肢力量健身器示意图。配重A 受到的重力为1200N,其底面积为5×10-2m2,B﹑C都是定滑轮,D是动滑轮;杠杆EH可绕O点在竖直平面内转动,OE:OH=2:5.小成受到的重力为600N,他通过细绳在H点施加竖直向下的拉力T1时,杠杆在水平位置平衡,小成对地面的压力为F1,配重A受到的拉力为FA1,配重A 对地面的压强P1为6×103Pa;小成在H点施加竖直向下的拉力为T2时,杠杆仍然在水平位置平衡,小成对地面的压力为F2,配重A受到的拉力为FA2,配重A对地面的压强P2为4×103 Pa。已知F1:F2=20:19,杠杆和细绳的质量均忽略不计。求∶(1)拉力FA1;(2)拉力T2;(3)动滑轮D受到的重力G.
古人曾设计如图所示的一种秤,来确定著名的“王冠之谜”中的王冠的含金量。AB为1m多长的秤杆,再正中o点支起,先在B端挂一块纯金样品,A端砝码盘中放与样品等重的砝码,秤杆平衡。当让金块浸没在水中时,砝码盘悬点A点移动到X点,秤杆平衡。记下X的位置。然后将样品改成纯银块,经过同样的操作并在秤杆上记下Y点。现将王冠挂到B端重复上述操作,在秤杆X,Y两点间Z点,XZ=a,YZ=b,则王冠中含金银之比即为b:a,试说明其原理。
如图所示,质量为70kg的工人站在水平地面上,用带有货箱的滑轮组把货物运到高处。第一次运送货物时,放入货箱的货物质量为160kg,工人用力F1匀速拉绳的功率为P1,货箱以0.1m/s的速度匀速上升,地面对工人的支持力为N1。第二次运送货物时,放人货箱的货物质量为120kg,工人用力F2匀速拉绳,货箱以0.2m/S的速度匀速上升,地面对工人的支持力为N2,滑轮组机械效率为η2。Nl与N2之比为15:19。(不计绳重及滑轮摩擦,g取10N/kg)求:(1)货箱和动滑轮的总质量m;(2)功率P1;(3)机械效率η2。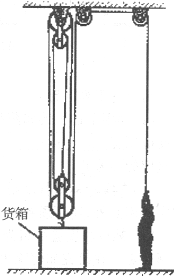
塔式起重机的结构如图所示,设机架重4×105牛,平衡块重2×105牛,轨道间的距离为4米。当平衡块距离中心线1米时,右侧轨道对轮子的作用力是左侧轨道对轮子作用力的2倍。现起重机挂钩在距离中心线10米处吊起重为105牛的重物时,把平衡块调节到距离中心线6米处,此时右侧轨道对轮子的作用力为多少N?
某人到健身房进行健身运动,用如图所示的牵引装置来锻炼腿部和手臂的力量。使用时:(1)绳子固定在A处,用手在B处用力FB拉绳子,使重物G匀速上升;(2)绳子固定在B处,用腿在A处用力FA拉绳子,使重物G匀速上升。以下结论正确的是(不考虑滑轮重和摩擦)( )
| A.FA>FB | B.FA<FB | C.FA=FB | D.条件不足,无法确定 |

你注意观察过家里的自行车吗?下列关于自行车增大摩擦或减小摩擦的说法,哪个是错误的?()
| A.轮胎上做有凸凹不平的花纹,是为了增大摩擦 |
| B.刹车时用力捏问是为了增大摩擦 |
| C.往车轮轴承上加润滑油是为了减小摩擦 |
| D.车轮上装有滚动轴承,是为了增大摩擦 |
试题篮
()