高中数学直线与方程试题

以 $(a_1,0)$ ， $(a_2,0)$ 为圆心的两圆均过 $(1,0)$ ，与 轴正半轴分别交于 $(y_1,0)$ ， $(y_2,0)$ ，且满足 $\ln y_1+\ln y_2=0$ ，则点 $(\frac{1}{a_1},\frac{1}{a_2})$ 的轨迹是（ ）

A．

直线

B．

圆

C．

椭圆

D．

双曲线

已知 $\{\begin{array}{c}2x+2y=-1\\ 4x+a^{2}y=a\end{array}$ ，当方程有无穷多解时， $a$ 的值为________．

设 $a\in R$，直线 $\mathit{ax}-y+2=0$和圆 $\left\{\begin{array}{c}x=2+2\cos \theta ,\\ y=1+2\sin \theta \end{array}\right.$（ $\theta$为参数）相切，则 $a$的值为_____________．

如图，一个湖的边界是圆心为O的圆，湖的一侧有一条直线型公路l ，湖上有桥AB（AB是圆O的直径）．规划在公路l上选两个点P、Q ，并修建两段直线型道路PB、QA ．规划要求:线段PB、QA上的所有点到点O的距离均不小于圆O的半径．已知点A、B到直线l的距离分别为AC和BD（C、D为垂足），测得AB=10，AC=6，BD=12（单位:百米）．

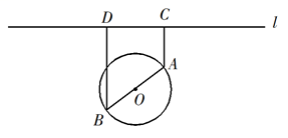
（1）若道路PB与桥AB垂直，求道路PB的长；   

（2）在规划要求下，P和Q中能否有一个点选在D处？并说明理由；   

（3）对规划要求下，若道路PB和QA的长度均为d（单位：百米）.求当d最小时，P、Q两点间的距离．

在平面直角坐标系 $\mathit{xOy}$ 中，P是曲线 $y=x+\frac{4}{x}(x>0)$ 上的一个动点，则点P到直线x+y=0的距离的最小值是________.

P（x，y）在线段AB上运动，已知A（2，4），B（5，﹣2），则的取值范围是（ ）

A．[﹣，]

B．（﹣∞，﹣]∪[，+∞）

C．[﹣，0）∁（0，]

D．（﹣，）

直线3x+倾斜角是（ ）

A．30°

B．60°

C．120°

D．135°

若直线与曲线相交于两点，则直线的倾斜角的取值范围是（    ）

A．	B．
C．	D．

已知点和在直线的两侧，则直线的倾斜角的取值范围是（  ）

A．

B．

C．

D．

直线经过点，点，则直线的倾斜角的大小是          .

直线与圆有公共点，则实数的取值范围是

A．

B．

C．

D．

直线的倾斜角为

A．

B．

C．

D．

直线的倾斜角的取值范围是（    ）

A．

B．

C．

D．

已知点和分别在直线的两侧，则直线倾斜角的取值范围是（  ）

A．

B．

C．

D．

过点引直线l与曲线相交于两点，为坐标原点，当的面积取最大值时，直线l的斜率等于              ．