初中数学因式分解-十字相乘法等试题

把多项式 $x^3+2x^2-3x$因式分解，结果为 　　．

分解因式： $2x^3-6x^2+4x=$　　．

分解因式： $b^4-b^2-12=$　     　．

将下列多项式因式分解，结果中不含有因式 $a+1$的是 $($　　 $)$

A． $a^2-1$B． $a^2+a$

C． $a^2+a-2$D． ${(a+2)}^2-2(a+2)+1$

把多项式 ${\mathit{x}}^{\mathit{2}}\mathit{+}\mathit{ax}\mathit{+}\mathit{b}$分解因式，得 $\mathit{(}\mathit{x}\mathit{+}\mathit{1}\mathit{)}\mathit{(}\mathit{x}\mathit{-}\mathit{3}\mathit{)}$，则 $\mathit{a}$， $\mathit{b}$的值分别是 $\mathit{(}$　　 $\mathit{)}$

A． $\mathit{a}\mathit{=}\mathit{-}\mathit{2}$， $\mathit{b}\mathit{=}\mathit{-}\mathit{3}$B． $\mathit{a}\mathit{=}\mathit{2}$， $\mathit{b}\mathit{=}\mathit{3}$C． $\mathit{a}\mathit{=}\mathit{-}\mathit{2}$， $\mathit{b}\mathit{=}\mathit{3}$D． $\mathit{a}\mathit{=}\mathit{2}$， $\mathit{b}\mathit{=}\mathit{-}\mathit{3}$

由多项式乘法： $(x+a)(x+b)=x^2+(a+b)x+\mathit{ab}$，将该式从右到左使用，即可得到“十字相乘法”进行因式分解的公式： $x^2+(a+b)x+\mathit{ab}=(x+a)(x+b)$．

示例：分解因式： $x^2+5x+6=x^2+(2+3)x+2\times 3=(x+2)(x+3)$．

（1）尝试：分解因式： $x^2+6x+8=(x+$　　 $\left)\right(x+$　　 $)$；

（2）应用：请用上述方法解方程： $x^2-3x-4=0$．

分解因式： $x^3-x^2-20x=$　　．

阅读理解：用“十字相乘法”分解因式 $2x^2-x-3$的方法．

（1）二次项系数 $2=1\times 2$；

（2）常数项 $-3=-1\times 3=1\times (-3)$，验算：“交叉相乘之和”；

$1\times 3+2\times (-1)=1$     $1\times (-1)+2\times 3=5$     $1\times (-3)+2\times 1=-1$     $1\times 1+2\times (-3)=-5$

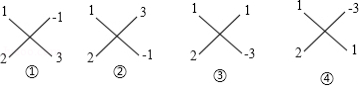
（3）发现第③个“交叉相乘之和”的结果 $1\times (-3)+2\times 1=-1$，等于一次项系数 $-1$．

即： $(x+1)(2x-3)=2x^2-3x+2x-3=2x^2-x-3$，则 $2x^2-x-3=(x+1)(2x-3)$．

像这样，通过十字交叉线帮助，把二次三项式分解因式的方法，叫做十字相乘法．仿照以上方法，分解因式： $3x^2+5x-12=$　　．

下列运算正确的是（　　）

A．	（a ^2+2b ^2）﹣2（﹣a ^2+b ^2）＝3a ^2+b ^2
B．	$\frac{a^2+1}{a-1}-a-1=\frac{2a}{a-1}$
C．	（﹣a） ^3 ^m÷a ^m＝（﹣1） ^ma ^2 ^m
D．	6x ^2﹣5x﹣1＝（2x﹣1）（3x﹣1）

分解因式：　　．

仔细阅读下面例题，解答问题：
例题：已知二次三项式x²﹣4x+m有一个因式是（x+3），求另一个因式以及m的值．
解：设另一个因式为（x+n），得
x²﹣4x+m=（x+3）（x+n）
则x²﹣4x+m=x²+（n+3）x+3n
∴．
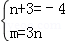解得：n=﹣7，m=﹣21
∴另一个因式为（x﹣7），m的值为﹣21
问题：仿照以上方法解答下面问题：
已知二次三项式2x²+3x﹣k有一个因式是（2x﹣5），求另一个因式以及k的值．

若x²+kx﹣15能分解为（x+5）（x﹣3），则k的值是（ ）

A．﹣2

B．2

C．﹣8

D．8

（1）计算：（2x²y）（-xy²z）³（3x²）
（2）因式分解：-8ax²+16axy-8ay²
（3）因式分解：（x²-3）²-4x²．

阅读材料，回答下列问题：
我们知道对于二次三项式这样的完全平方式，可以用公式将它分解成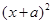的形式，但是，对于二次三项式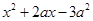就不能直接用完全平方公式，可以采用如下方法：
＝＝．
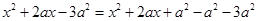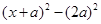像上面这样把二次三项式分解因式的数学方法是配方法．请同学们借助这种数学思想方法把多项式分解因式．

因式分解
（1）3x-3x³
（2）2a³b-12a²b+18ab
（3）x²+2x-3．