如图,3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,则20条直线两两相交最多有 个交点.
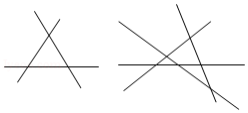
小星在"趣味数学"社团活动中探究了直线交点个数的问题.现有7条不同的直线 ,2,3,4,5,6, ,其中 , ,则他探究这7条直线的交点个数最多是
| A. |
17个 |
B. |
18个 |
C. |
19个 |
D. |
21个 |
如图所示,1条直线将平面分成2个部分,2条直线最多可将平面分成4个部分,3条直线最多可将平面分成7个部分,4条直线最多可将平面分成11个部分.现有n条直线最多可将平面分成56个部分,则n的值为 .
我们定义:平面内两条直线l1、l2相交于点O(l1与l2不垂直),对于该平面内任意一点P,如果点P到直线l1、l2的距离分别为a、b,那么有序实数对(a,b)就叫做点P的“平面斜角坐标”.如果常数m、n都是正数,那么在平面内与“平面斜角坐标”(m,n)对应的点共有__________个.
挑游戏棒是一种好玩的游戏,游戏规则:当一根棒条没有被其它棒条压着时,就可以把它往上拿走.如图中,按照这一规则,第1次应拿走⑨号棒,第2次应拿走⑤号棒,…,则第6次应拿走()
| A.②号棒 | B.⑦号棒 | C.⑧号棒 | D.⑩号棒 |
如图,平面上有四个点A、B、C、D,根据下列语句画图.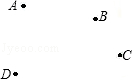
(1)画直线AB;
(2)作射线BC;
(3)画线段CD;
(4)连接AD,并将其反向延长至E,使DE=2AD;
(5)找到一点F,使点F到A、B、C、D四点距离和最短.
如图,在同一个平面内有四个点A、B、C、D.
①画射线CD;②画直线AD;③连接AB;④直线BD与直线AC相交于点O.
同一平面内互不重合的三条直线的交点的个数是()
| A.可能是0个,1个,2个 |
| B.可能是0个,2个,3个 |
| C.可能是0个,1个,2个或3个 |
| D.可能是1个可3个 |
观察图形,并阅读相关的文字:
那么8条直线相交,最多可形成交点的个数是()
| A.21 | B.28 | C.36 | D.45 |
下列说法中正确的是().
| A.角是由两条射线组成的图形 |
| B.一条射线就是一个周角 |
| C.两条直线相交,只有一个交点 |
| D.如果线段AB=BC,那么B叫做线段AB的中点 |
试题篮
()