小学数学年、月、日及其关系、单位换算与计算试题

计算： 

如图一只甲虫从画有方格的木板上的A点出发，沿着一段一段的横线、竖线爬行到B，图1中的路线对应下面的算式：.请在下面右图中用粗线画出对应于算式：的路线．

国际统一书号ISBN由10个数字组成，前面9个数字分成3组，分别用来表示区域、出版社和书名，最后一个数字则作为核检之用。核检码可以根据前9个数字按照一定的顺序算得。如：某书的书号是ISBN 7-107-17543-2，它的核检码的计算顺序是：
①7×10＋1×9＋0×8＋7×7＋1×6＋7×5＋5×4＋4×3＋3×2＝207；
②207÷11＝18……9；   
③11－9＝2。这里的2就是该书号的核检码。
依照上面的顺序，求书号ISBN-7-303-07618-□的核检码。

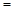
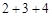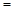
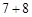“⊙”表示一种新的运算符号，已知：2⊙3；7⊙2：3⊙5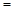，……按此规则，如果n⊙8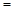68，那么，n ____.

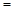定义运算“⊙”如下:
对于两个自然数a和b,它们的最大公约数与最小公倍数的差记为a⊙b.
比如:10和14,最小公倍数为70,最大公约数为2,则10⊙14=70-2=68.
(1)求12⊙21,5⊙15;
(2)说明,如果c整除a和b,则c也整除a⊙b;如果c整除a和a⊙b,则c也整除b;
(3)已知6⊙x=27,求x的值.

设a,b是两个非零的数,定义a※b.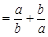
(1)计算(2※3)※4与2※(3※4).
(2)如果已知a是一个自然数,且a※3=2,试求出a的值. 

两个不等的自然数a和b,较大的数除以较小的数,余数记为a☉b,比如5☉2=1,7☉25=4,6☉8="2." （8级）
(1)求1991☉2000,(5☉19)☉19,(19☉5)☉5;
(2)已知11☉x=2,而x小于20,求x;
(3)已知(19☉x)☉19=5,而x小于50,求x.

对于任意的两个自然数和，规定新运算： ，其中、表示自然数.⑴求1100的值；⑵已知1075，求为多少？⑶如果（3）2121，那么等于几？

x、y表示两个数，规定新运算“*”及“△”如下：x*y=mx+ny，x△y=kxy，其中 m、n、k均为自然数，已知 1*2=5，（2*3）△4=64，求（1△2）*3的值.

对于任意有理数x, y,定义一种运算“※”，规定:x※y=,其中的表示已知数,等式右边是通常的加、减、乘运算.又知道1※2=3,2※3=4,x※m=x(m≠0),则m的数值是 _________.

在计算机中，对于图中的数据(或运算)的读法规则是：先读第一分支圆圈中的，再读与它相连的第二分支左边的圆圈中的，最后读与它相连的第二分支右边的圆圈中的，也就是说，对于每一个圆圈中的数据(或运算)都是按"中→左→右"的顺序。如：图A表示：2+3， B表示2+3×2－1。图C中表示的式子的运算结果是________ 。

如果、、是3个整数，则它们满足加法交换律和结合律，即
⑴a+b=b+a；⑵。
现在规定一种运算"*"，它对于整数a、 b、c 、d 满足：
（a，b）*（c，d）=（a×c+b×d，a×c-b×d）。
例： 
请你举例说明，"*"运算是否满足交换律、结合律。

已知：10△3=14， 8△7=2， △，根据这几个算式找规律，如果
△=1，那么=              .

一个数n的数字中为奇数的那些数字的和记为，为偶数的那些数字的和记为，例如，．
        ；＝      ．

规定△, 计算：（2△1）（11△10）______.