某池塘中野生水葫芦的面积与时间的函数关系的图象,如图所示.假设其关系为指数函数,并给出下列说法:

①此指数函数的底数为 ;
;
②在第 个月时,野生水葫芦的面积就会超过
个月时,野生水葫芦的面积就会超过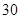
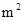 ;
;
③野生水葫芦从
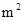 蔓延到
蔓延到
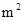 只需
只需 个月;
个月;
④设野生水葫芦蔓延到
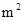 ,
,
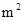 ,
,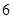
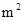 所需的时间分别为
所需的时间分别为 ,
, ,
,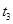 ,则有
,则有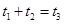 ;
;
⑤野生水葫芦在第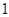 到第
到第 个月之间蔓延的平均速度等于在第
个月之间蔓延的平均速度等于在第 到第
到第 个月之间蔓延的平均速度.
个月之间蔓延的平均速度.
其中正确的说法有 .(请把正确说法的序号都填在横线上)
下面是两个变量的一组数据:
| X |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
则这两个变量之间的线性回归方程是( )
A.y=-16+9x B.y=31-x C.y=30-x D.y=-15+9x
某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,用最小二乘法求出y与x的回归方程 ;
;
(3)预测销售额为115万元时,大约需要多少万元广告费。
参考公式:回归方程为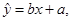 其中
其中 ,
, 
在一次数学实验中,运用计算器采集到如下一组数据:
| x |
-2.0 |
-1.0 |
0 |
1.00 |
2.00 |
3.00 |
| y |
0.24 |
0.51 |
1 |
2.02 |
3.98 |
8.02 |
则x,y的函数关系与下列哪类函数最接近(其中,a,b为待定系数)( )
A.y=a+bx B.y=a+bx
C.y=a+logbx D.y=a+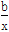
某单位为了了解用电量 度与气温
度与气温
 之间的关系,随机统计了某
之间的关系,随机统计了某 天的用电量与当天气温,并制作了对照表
天的用电量与当天气温,并制作了对照表

由表中数据得回归直线方程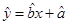 中
中 ,预测当气温为
,预测当气温为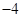
 时,用电量的度数是 .
时,用电量的度数是 .
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗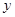 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
 |
3 |
4 |
5 |
6 |
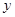 |
2.5 |
3 |
4 |
4.5 |
( )
)
(1)请根据上表提供的数据,用最小二乘法求出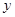 关于
关于 的线性回归方程
的线性回归方程 ;
;
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
.已知某种产品的支出广告额 与利润额
与利润额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
| x |
3 |
4 |
5 |
6 |
7 |
| y |
20 |
30 |
30 |
40 |
60 |
则回归直线方程必过( )
A.(5,30) B.(4,30) C.(5,35) D.(5,36)
某种产品的广告费支出x与销售额y之间有如下对应数据(单位:百万元).
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
t |
70 |
根据上表求出y关于x的线性回归方程为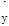 =6.5x+17.5,则表中t的值为_ .
=6.5x+17.5,则表中t的值为_ .
下图所给4个图象中,与所给3件事吻合最好的顺序为( )
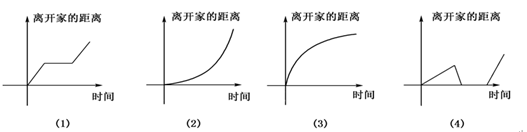
(1)小明离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)小明骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)小明出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
| A.(1)(2)(4) | B.(4)(2)(3) | C.(4)(1)(3) | D.(4)(1)(2) |
(本小题满分12分)
某研究机构对高三学生的记忆力 和判断力
和判断力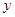 进行统计分析,得下表数据:
进行统计分析,得下表数据:
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
(1)画出散点图并指出 与
与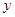 之间是正相关还是负相关 ;
之间是正相关还是负相关 ;
(2)请根据上表提供的数据,用最小二乘法求出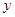 关于
关于 的线性回归方程
的线性回归方程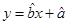 ;
;
其中(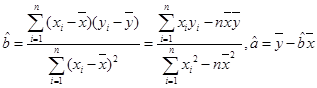 )
)
(3)记忆力为14的同学的判断力约为多少?
试题篮
()