如图所示,ABC为与匀强磁场垂直的边长为 的等边三角形,比荷为
的等边三角形,比荷为 的电子以速度
的电子以速度 0从A点沿AB边出射,欲使电子经过BC边,则磁感应强度B的取值为 [ ]
0从A点沿AB边出射,欲使电子经过BC边,则磁感应强度B的取值为 [ ]
A. |
B. |
C. |
D. |
半径为R的圆形空间内,存在着垂直于纸面向里的匀强磁场,一个带电粒子(不计重力)从A点以速度v0垂直于磁场方向射入磁场中,并从B点射出.∠AOB=120°,如图所示,则该带电粒子在磁场中运动的时间为( )
A. |
B. |
C. |
D. |
如图所示,在垂直纸面向里的匀强磁场的边界上,有两个电荷量绝对值相同、质量相同的正、负粒子(不计重力),从A点以相同的速度先后射入磁场中,入射方向与边界成θ角,则正、负粒子在磁场中( )
| A.运动时间相同 |
| B.运动轨迹的半径相同 |
| C.重新回到边界时速度大小和方向相同 |
| D.重新回到边界时与A点的距离相等 |
(17分)如图所示的平面直角坐标系xOy,在第Ⅰ象限内有平行于y轴的匀强电场,方向沿y正方向;在第Ⅳ象限的正方形abcd区域内有匀强磁场,方向垂直于xOy平面向里,正方形边长为L且ad边与x轴重合,ab边与y轴平行.一质量为m、电荷量为q的粒子,从y轴上的P(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第Ⅳ象限的磁场区域,不计粒子所受的重力.求:
(1)电场强度E的大小;
(2)粒子到达a点时速度的大小和方向;
(3)磁感应强度B满足什么条件,粒子经过磁场后能到达y轴上,且速度与y轴负方向成450角?
(4)磁感应强度B满足什么条件,粒子经过磁场后不能到达y轴上?
(4分)如图所示,矩形区域宽度为l,其内有磁感应强度为B、垂直纸面向外的匀强磁场.一带电粒子以初速度v0垂直左边界射入,飞出磁场时偏离原方向300.若撤去原来的磁场,在此区域内加一个电场强度为E、方向竖直向下的匀强电场(图中未画出),带电粒子仍以原来的初速度入射.不计粒子的重力,求:
(1)带电粒子在磁场中的运动半径;
(2)带电粒子在磁场中运动的时间;
(3)带电粒子飞出电场后的偏转角.
如图所示,在xOy平面内存在着磁感应强度大小为B的匀强磁场,第一、二、四象限内的磁场方向垂直纸面向里,第三象限内的磁场方向垂直纸面向外。P(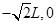 )、Q(
)、Q(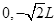 )为坐标轴上的两个点。现有一电子从P点沿PQ方向射出,不计电子的重力:( )
)为坐标轴上的两个点。现有一电子从P点沿PQ方向射出,不计电子的重力:( )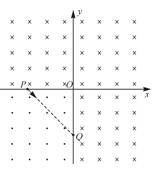
A.若电子从P点出发恰好经原点O第一次射出磁场分界线,则电子运动的路程一定为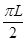 |
B.若电子从P点出发经原点O到达Q点,则电子运动的路程一定为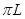 |
C.若电子从P点出发经原点O到达Q点,则电子运动的路程一定为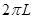 |
D.若电子从P点出发经原点O到达Q点,则电子运动的路程可能为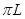 ,也可能为 ,也可能为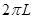 |
如图, OAC的三个顶点的坐标分别为O(0,0)、A(0,L)、C(
OAC的三个顶点的坐标分别为O(0,0)、A(0,L)、C( ,0),在
,0),在 OAC区域内有垂直于xOy平面向里的匀强磁场。在t=0时刻,同时从三角形的OA边各处以沿y轴正向的相同速度将质量均为m,电荷量均为q的带正电粒子射入磁场,已知在t=t0时刻从OC边射出磁场的粒子的速度方向垂直于y轴。不计粒子重力和空气阻力及粒子间相互作用。
OAC区域内有垂直于xOy平面向里的匀强磁场。在t=0时刻,同时从三角形的OA边各处以沿y轴正向的相同速度将质量均为m,电荷量均为q的带正电粒子射入磁场,已知在t=t0时刻从OC边射出磁场的粒子的速度方向垂直于y轴。不计粒子重力和空气阻力及粒子间相互作用。
(1)求磁场的磁感应强度B的大小;
(2)若从OA边两个不同位置射入磁场的粒子,先后从OC边上的同一点P(P点图中未标出)射出磁场,求这两个粒子在磁场中运动的时间t1与t2之间应满足的关系;
(3)从OC边上的同一点P射出磁场的这两个粒子经过P点的时间间隔与P点位置有关,若该时间间隔最大值为 ,求粒子进入磁场时的速度大小。
,求粒子进入磁场时的速度大小。
如图所示,在矩形区域abcd内充满垂直纸面向里的匀强磁场,磁感应强度为B,在ad边中点的粒子源,在t=0时刻垂直于磁场发射出大量的同种带电粒子,所有粒子的初速度大小相同,方向与od的夹角分布在0~180°范围内。已知沿od方向发射的粒子在t=t0时刻刚好从磁场边界cd上的p点离开磁场,ab=1.5L,bc=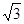 L,粒子在磁场中做圆周运动的半径R=L,不计粒子的重力和粒子间的相互作用,求:
L,粒子在磁场中做圆周运动的半径R=L,不计粒子的重力和粒子间的相互作用,求: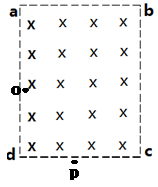
(1)粒子在磁场中的运动周期T和粒子的比荷q/m;
(2)粒子在磁场中运动的最长时间;
(3)t=t0时刻仍在磁场中的粒子所处位置在某一圆弧上,在图中画出该圆弧并说明圆弧的圆心位置以及圆心角大小;
如图所示,在真空中坐标xOy面的x>0区域内,有磁感应强度B=1.0×10-2T的匀强磁场,方向与xOy平面垂直,在x轴上的P(10,0)点处有一放射源,在xOy平面内向各个方向发射速率为v=1.0×105m/s的带正电粒子,粒子的质量为m=1.0×10-26kg,粒子带电量为q=1.0×10-18C,则带电粒子能打到y轴上的范围是(重力的影响不计)( )
| A.-10cm≤y≤10cm |
B.-10cm≤y≤ cm cm |
C. cm≤y≤ cm≤y≤ cm cm |
D. cm≤y≤10cm cm≤y≤10cm |
长为L的水平极板间,有垂直纸面向内的匀强磁场,如图所示,磁感强 度为B,板间距离也为L,板不带电,现有质量为m,电量为q的带正电粒子(不计重力),从左边极板间中点处垂直磁感线以速度v水平射入磁场,欲使粒子不打在极板上,可采用的办法是
| A.使粒子的速度v<BqL/4m |
| B.使粒子的速度v>5BqL/4m |
| C.使粒子的速度v>BqL/m |
| D.使粒子速度BqL/4m<v<5BqL/4m |
如图所示,以直角三角形AOC 为边界的有界匀强磁场区域,磁感应强度为B,∠A=60°,AO=a.在O 点放置一个粒子源,可以向各个方向发射某种带负电粒子,粒子的比荷为q/m,发射速度大小都为v0,且满足v0= ,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是( )
,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是( )
| A.粒子有可能打到A 点 |
| B.以θ=60°飞入的粒子在磁场中运动时间最短 |
| C.以θ<30°飞入的粒子在磁场中运动的时间都相等 |
| D.在AC 边界上只有一半区域有粒子射出 |
如图所示,在半径为R圆形区域有垂直于纸面向里、磁感应强度为B的匀强磁场,从A点沿着AO方向垂直磁场射入大量带正电、电荷量为q、质量为m、速率不同的粒子,不计粒子间的相互作用力和重力,关于这些粒子在磁场中的运动以下说法正确的是( )
| A.这些粒子出射方向的反向延长线不一定过O点 |
| B.速率越大的粒子在磁场中通过的弧长越长,时间也越长 |
| C.这些粒子在磁场中的运动时间相同 |
| D.若粒子速率满足v=qBR/m,则粒子出射方向与入射方向垂直 |
如图所示,在光滑绝缘的水平面内,对角线AC将边长为L的正方形分成ABC和ADC两个区域,ABC区域有垂直于水平面的匀强磁场,ADC区域有平行于DC并由C指向D的匀强电场.质量为m、带电量为+q的粒子从A点沿AB方向以v的速度射入磁场区域,从对角线AC的中点O进入电场区域.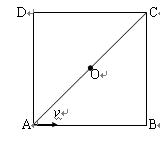
(1)判断磁场的方向并求出磁感应强度B的大小.
(2)讨论电场强度E在不同取值时,带电粒子在电场中运动的时间t.
如图所示,在以坐标原点O为圆心.半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。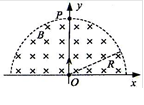
(1)求电场强度的大小和方向。
(2)若仅撤去磁场,带电粒子仍从O点以相同的速度射入,经 时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
(3)若仅撤去电场,带电粒子仍从O点射入,且速度为原来的4倍,
求粒子在磁场中运动的时间。
在边长为2a的正△ABC内存在垂直纸面向里的磁感强度为B的匀强磁场,有一带正电q,质量为m的粒子从距A点 的D点垂直AB方向进入磁场,如下图所示,求:
的D点垂直AB方向进入磁场,如下图所示,求: 
(1)粒子速率应满足什么条件,粒子能从AB间射出;
(2)粒子速率应满足什么条件,粒子能从AC间射出。
试题篮
()