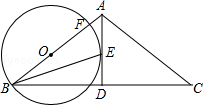
如图,在△ABC中,AB=AC,AD是角平分线,BE平分∠ABC交AD于点E,点O在AB上,以OB为半径的⊙O经过点E,交AB于点F
(1)求证:AD是⊙O的切线;
(2)若AC=4,∠C=30°,求 的长.
如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是 .

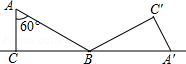
如图,△ABC中,∠C=90°,∠A=60°, .将△ABC沿直线CB向右作无滑动滚动一次,则点C经过的路径长是 .
如图,以点 O为圆心的两个同心圆中,大圆的弦 AB是小圆的切线,点 P为切点, , OP=6,则劣弧 AB的长为 .

如图,在矩形 中, , ,以点 为圆心, 长为半径画弧交边 于点 ,连接 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
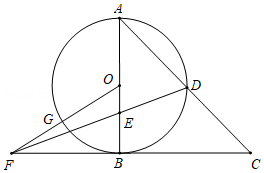
如图,在 中, , ,以 为直径的 交 于点 ,点 为线段 上的一点, ,连接 并延长交 的延长线于点 ,连接 交 于点 ,若 ,则 的长是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在四边形 中, , ,我们把这种两组邻边分别相等的四边形叫做“筝形”.筝形 的对角线 , 相交于点 .以点 为圆心, 长为半径画弧,分别交 , 于点 , .若 , ,则 的长为 (结果保留 .

如图,将 绕点 顺时针旋转 得到 ,点 的对应点 恰好落在 的延长线上,连接 .
(1)求证: ;
(2)若 , ,求 , 两点旋转所经过的路径长之和.

如图,等边中,
,点
,点
分别是边
,
上的动点,且
,连接
、
交于点
,当点
从点
运动到点
时,则点
的运动路径的长度为 .

试题篮
()