初中数学轴对称-最短路线问题试题

如图，CD是⊙O的直径， $\mathit{CD}＝4$， $\angle \mathit{ACD}＝20°$，点B为弧AD 的中点，点P是直径CD 上的一个动点，则PA+PB的最小值为　　．

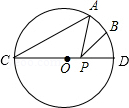
如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ ABC的三个顶点的坐标分别为 A（﹣1，3）， B（﹣4，0）， C（0，0）

（1）画出将△ ABC向上平移1个单位长度，再向右平移5个单位长度后得到的△ A ₁ B ₁ C ₁；

（2）画出将△ ABC绕原点 O顺时针方向旋转90°得到△ A ₂ B ₂ O；

（3）在 x轴上存在一点 P，满足点 P到 A ₁与点 A ₂距离之和最小，请直接写出 P点的坐标．

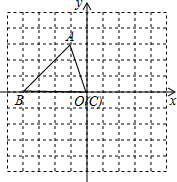
如图所示，正方形ABCD的边长为4，E是边BC上的一点，且 $\mathit{BE}＝1$，P是对角线AC上的一动点，连接PB、PE，当点P在AC上运动时，△PBE周长的最小值是　　．

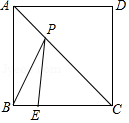
如图，在四边形 ABCD中，∠ B＝∠ C＝90°， AB＞ CD， AD＝ AB+ CD．

（1）利用尺规作∠ ADC的平分线 DE，交 BC于点 E，连接 AE（保留作图痕迹，不写作法）；

（2）在（1）的条件下，

①证明： AE⊥ DE；

②若 CD＝2， AB＝4，点 M， N分别是 AE， AB上的动点，求 BM+ MN的最小值．

如图，△ ABC中， AC＝ BC＝3， AB＝2，将它沿 AB翻折得到△ ABD，点 P、 E、 F分别为线段 AB、 AD、 DB上的动点，则 PE+ PF的最小值是（　　）

A．

$\frac{\sqrt{10}}{3}$

B．

$\frac{2\sqrt{2}}{3}$

C．

$\frac{4\sqrt{2}}{3}$

D．

$\frac{8\sqrt{10}}{3}$

如图，已知 A（ $\frac{1}{2}$ ， y ₁）， B（2， y ₂）为反比例函数 y＝ $\frac{1}{x}$ 图象上的两点，动点 P（ x，0）在 x轴的正半轴上运动，当线段 AP与线段 BP之差达到最大时点 P的坐标是（　　）

A．

（ $\frac{7}{2}$ ，0）

B．

（3，0）

C．

（4，0）

D．

（ $\frac{5}{2}$ ，0）

如图，在平面直角坐标系中，反比例函数 y＝ $\frac{k}{x}$ （ k＞0）的图象与半径为5的⊙ O交于 M、 N两点，△ MON的面积为3.5，若动点 P在 x轴上，则 PM+ PN的最小值是 　　．

如图，直线 $y＝x+4$与双曲线 $y=\frac{\text{k}}{\text{x}}(k\ne 0)$相交于 $A\mathit{（﹣}1，a）$、B两点，在y轴上找一点P，当 $\mathit{PA}+\mathit{PB}$的值最小时，点P的坐标为　　．

如图，在Rt△ ABC中，∠ C＝90°， AC＝3， BC＝4， D、 E分别是 AB、 BC边上的动点，则 AE+ DE的最小值为（　　）

A．

$\frac{48}{5}$

B．

$\frac{24}{5}$

C．

5

D．

$\frac{12}{5}$

如图，菱形 ABCD的边长为2 cm，∠ A＝120°，点 E是 BC边上的动点，点 P是对角线 BD上的动点，若使 PC+ PE的值最小，则这个最小值为 　　．

如图，在周长为12的菱形中，，，若为对角线上一动点，则的最小值为　　

A．1B．2C．3D．4

如图，矩形的边OA在x轴上，边OC在y轴上，点B的坐标为（10，8），沿直线OD折叠矩形，使点A正好落在BC上的E处，E点坐标为（6，8），抛物线y＝ax²+bx+c经过O、A、E三点．

（1）求此抛物线的解析式；

（2）求AD的长；

（3）点P是抛物线对称轴上的一动点，当△PAD的周长最小时，求点P的坐标．

如图，已知一次函数 $y=\frac{1}{2}x+b$的图象与反比例函数 $y=\frac{\text{k}}{\text{x}}(x<0)$的图象交于点A（﹣1，2）和点B，点C在y轴上．

（1）当△ABC的周长最小时，求点C的坐标；

（2）当x+b＜时，请直接写出x的取值范围．

如图，正△ABC的边长为2，过点B的直线l⊥AB，且△ABC与△A′BC′关于直线l对称，D为线段BC′上一动点，则AD+CD的最小值是（　　）

A．4B． $3\sqrt{2}$C． $2\sqrt{3}$D． $2+\sqrt{3}$

如图， $\mathit{\Delta ABC}$ 为等边三角形，边长为6， $\mathit{AD}\perp \mathit{BC}$ ，垂足为点 $D$ ，点 $E$ 和点 $F$ 分别是线段 $\mathit{AD}$ 和 $\mathit{AB}$ 上的两个动点，连接 $\mathit{CE}$ ， $\mathit{EF}$ ，则 $\mathit{CE}+\mathit{EF}$ 的最小值为 　 　．