为了倡导“节约用水,从我做起”,某市政府决定对该市直属机关200户家庭用水情况进行调查.市政府调查小组随机抽查了其中部分家庭一年的月平均用水量(单位:吨),调查中发现,每户家庭月平均用水量在 吨范围内,并将调查结果制成了如下尚不完整的统计表:
月平均用水量(吨 |
3 |
4 |
5 |
6 |
7 |
频数(户数) |
4 |
|
9 |
10 |
7 |
频率 |
0.08 |
0.40 |
|
|
0.14 |
请根据统计表中提供的信息解答下列问题:
(1)填空: , , .
(2)这些家庭中月平均用水量数据的平均数是 ,众数是 ,中位数是 .
(3)根据样本数据,估计该市直属机关200户家庭中月平均用水量不超过5吨的约有多少户?
(4)市政府决定从月平均用水量最省的甲、乙、丙、丁四户家庭中,选取两户进行“节水”经验分享.请用列表或画树状图的方法,求出恰好选到甲、丙两户的概率,并列出所有等可能的结果.
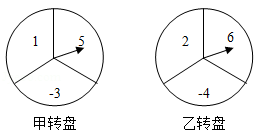
如图,甲、乙两个转盘均被分成3个面积相等的扇形,每个扇形中都标有相应的数字,同时转动两个转盘(当指针指在边界线上时视为无效,需重新转动转盘),当转盘停止后,把甲、乙两个转盘中指针所指数字分别记为 , .请用树状图或列表法求点 落在平面直角坐标系第一象限内的概率.
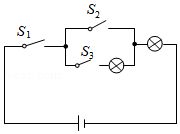
如图所示,电路连接完好,且各元件工作正常.随机闭合开关 , , 中的两个,能让两个小灯泡同时发光的概率是 .
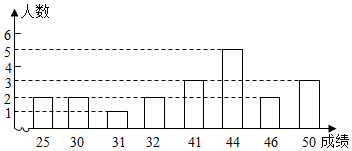
某大学为了解大学生对中国共产党党史知识的学习情况,在大学一年级和二年级举行有关党史知识测试活动.现从一、二两个年级中各随机抽取20名学生的测试成绩(满分50分,30分及30分以上为合格;40分及40分以上为优秀)进行整理、描述和分析,给出了下面的部分信息.
大学一年级20名学生的测试成绩为:
39,50,39,50,49,30,30,49,49,49,43,43,43,37,37,37,43,43,37,25.
大学二年级20名学生的测试成绩条形统计图如图所示;两个年级抽取的学生的测试成绩的平均数、众数、中位数、优秀率如下表所示:
年级 |
平均数 |
众数 |
中位数 |
优秀率 |
大一 |
|
|
43 |
|
大二 |
39.5 |
44 |
|
|
请你根据上面提供的所有信息,解答下列问题:
(1)上表中 , , , , ;
根据样本统计数据,你认为该大学一、二年级中哪个年级学生掌握党史知识较好?并说明理由(写出一条理由即可);
(2)已知该大学一、二年级共1240名学生参加了此次测试活动,通过计算,估计参加此次测试活动成绩合格的学生人数能否超过1000人;
(3)从样本中测试成绩为满分的一、二年级的学生中随机抽取两名学生,用列举法求两人在同一年级的概率.
某学校九年级有12个班,每班50名学生,为了调查该校九年级学生平均每天的睡眠时间,准备从12个班里抽取50名学生作为一个样本进行分析,并规定如下:设每个学生平均每天的睡眠时间为 (单位,小时),将收集到的学生平均每天睡眠时间按 、 、 分为三类进行分析.
(1)下列抽取方法具有代表性的是 .
.随机抽取一个班的学生
.从12个班中,随机抽取50名学生
.随机抽取50名男生
.随机抽取50名女生
(2)由上述具有代表性的抽取方法抽取50名学生,平均每天的睡眠时间数据如表:
睡眠时间 (小时) |
5 |
5.5 |
6 |
6.5 |
7 |
7.5 |
8 |
8.5 |
人数(人 |
1 |
1 |
2 |
10 |
15 |
9 |
10 |
2 |
①这组数据的众数和中位数分别是 , ;
②估计九年级学生平均每天睡眼时间 的人数大约为多少;
(3)从样本中学生平均每天眠时间 的4个学生里,随机抽取2人,画树状图或列表,求抽得2人平均每天睡眠时间都是6小时的概率.
李老师为缓解小如和小意的压力,准备了四个完全相同(不透明)的锦囊,里面各装有一张纸条,分别写有: .转移注意力, .合理宣泄, .自我暗示, .放松训练.
(1)若小如随机取走一个锦囊,则取走的是写有“自我暗示”的概率是 ;
(2)若小如和小意每人先后随机抽取一个锦囊(取走后不放回),请用列表法或画树状图的方法求小如和小意都没有取走“合理宣泄”的概率.
为迎接建党100周年,某校组织学生开展了党史知识竞赛活动.竞赛项目有: .回顾重要事件; .列举革命先烈; .讲述英雄故事; .歌颂时代精神.学校要求学生全员参加且每人只能参加一项,为了解学生参加竞赛情况,随机调查了部分学生,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中信息解答下列问题:
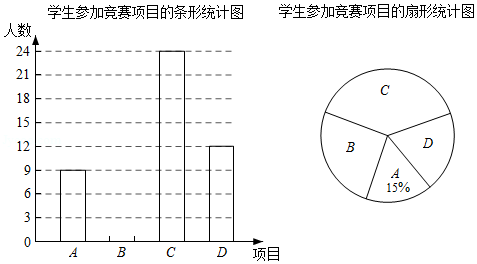
(1)本次被调查的学生共有 名;
(2)在扇形统计图中" 项目"所对应的扇形圆心角的度数为 ,并把条形统计图补充完整;
(3)从本次被调查的小华、小光、小艳、小萍这四名学生中,随机抽出2名同学去做宣讲员,请用列表或画树状图的方法求出恰好小华和小艳被抽中的概率.
为庆祝建党100周年,某大学组织志愿者周末到社区进行党史学习宣讲,决定从 , , , 四名志愿者中通过抽签的方式确定两名志愿者参加.抽签规则:将四名志愿者的名字分别写在四张完全相同不透明卡片的正面,把四张卡片背面朝上,洗匀后放在桌面上,先从中随机抽取一张卡片,记下名字,再从剩余的三张卡片中随机抽取第二张,记下名字.
(1)“ 志愿者被选中”是 事件(填“随机”或“不可能”或“必然” ;
(2)请你用列表法或画树状图法表示出这次抽签所有可能的结果,并求出 , 两名志愿者被选中的概率.
一张圆桌旁设有4个座位,丙先坐在了如图所示的座位上,甲、乙2人等可能地坐到①、②、③中的2个座位上.
(1)甲坐在①号座位的概率是 ;
(2)用画树状图或列表的方法,求甲与乙相邻而坐的概率.

圆周率 是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对 有过深入的研究.目前,超级计算机已计算出 的小数部分超过31.4万亿位.有学者发现,随着 小数部分位数的增加, 这10个数字出现的频率趋于稳定接近相同.
(1)从 的小数部分随机取出一个数字,估计数字是6的概率为 ;
(2)某校进行校园文化建设,拟从以上4位科学家的画像中随机选用2幅,求其中有一幅是祖冲之的概率.(用画树状图或列表方法求解)

把4张分别写有数字1、2、3、4的卡片(卡片的形状、大小、质地都相同)放在盒子中,搅匀后从中任意取出1张卡片,记录后放回、搅匀,再从中任意取出1张卡片.求下列事件发生的概率.(请用“画树状图”或“列表”等方法写出分析过程)
(1)取出的2张卡片数字相同;
(2)取出的2张卡片中,至少有1张卡片的数字为“3”.
即将举行的2022年杭州亚运会吉祥物"宸宸"、"琮琮"、"莲莲",将三张正面分别印有以上3个吉祥物图案的卡片(卡片的形状、大小、质地都相同)背面朝上、洗匀.

(1)若从中任意抽取1张,抽得卡片上的图案恰好为"莲莲"的概率是 .
(2)若先从中任意抽取1张,记录后放回,洗匀,再从中任意抽取1张,求两次抽取的卡片图案相同的概率.(请用树状图或列表的方法求解)
试题篮
()