初中数学应用类问题试题

下列四个命题：
①等边三角形是中心对称图形；
②在同圆或等圆中，相等的弦所对的圆周角相等；
③三角形有且只有一个外接圆；
④垂直于弦的直径平分弦所对的两条弧．
其中真命题的个数有（　　）
　 

A．1个

B．2个

C．3个

D．4个

一个圆锥形的漏斗，小李用三角板测得其高度的尺寸如图所示，那么漏斗的斜壁AB的长度为  cm．

如图，量角器外缘上有A、B两点，它们所表示的读数分别是80°、50°，则∠ACB应为  ．

用一把带有刻度的直尺，①可以画出两条平行的直线与b，如图⑴；②可以画出∠AOB的平分线OP，如图⑵所示；③可以检验工件的凹面是否为半圆，如图⑶所示；④可以量出一个圆的半径，如图⑷所示．这四种说法正确的个数有                 （      ）

A．1个

B．2个

C．3个

D．4个

已知圆锥的底面半径为1cm，母线长为3cm，则其全面积为              （    ）

A．π

B．3π

C．4π

D．7π

如图，是由形状相同的正六边形和正三角形镶嵌而成的一组有规律的图案，则第n个图案中阴影小三角形的个数是        ．

如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（1，1），（1，2），（2，2）…根据这个规律，第2012个点的横坐标为        ．

一个由小菱形组成的装饰链，断去了一部分，剩下部分如图所示，则断去部分的小菱形的个数可能是【   】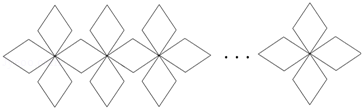

A．3

B．4

C．5

D．6

如图，在平面直角坐标系中，,,,,……，以为对角线作第一个正方形，以为对角线作第二个正方形，以为对角线作第三个正方形，……，顶点，，，……都在第一象限，按照这样的规律依次进行下去，点的坐标为_________________．
               

正方形网格中，每个小正方形的边长为1．图1所示的矩形是由4个全等的直角
梯形拼接而成的（图形的各顶点都在格点上；拼接时图形互不重叠，不留空隙），如果用这
4个直角梯形拼接成一个等腰梯形，那么（1）仿照图1，在图2中画出一个拼接成的等腰梯
形；（2）这个拼接成的等腰梯形的周长为________．

一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是   

同一时刻，身高1.6米的小强在阳光下的影长为0.8米，一棵大树的影长为4.8米，则这棵树的高度为

A．2.4米

B．9.6米

C．2米

D．1.6米

某研究性学习小组在探究矩形的折纸问题时，将一块直角三角板的直角顶点绕矩形ABCD（AB＜BC）的对角线的交点O旋转（①→②→③），图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点。
该学习小组成员意外的发现图①（三角板一直角边与OD重合）中，BN²=CD²+CN²，在图③中（三角板一边与OC重合），CN²=BN²+CD²，请你对这名成员在图①和图③中发现的结论选择其一说明理由。
试探究图②中BN、CN、CM、DN这四条线段之间的数量关系，写出你的结论，并说明理由。
将矩形ABCD改为边长为1的正方形ABCD，直角三角板的直角顶点绕O点旋转到图④，两直角边与AB、BC分别交于M、N，直接写出BN、CN、CM、DM这四条线段之 间所满足的数量关系（不需要证明）

一个几何体的三视图如图所示，网格中小正方形的边长均为1，那么下列选项中最接近这个几何体的侧面积的是（   ）

A．24.0

B．62.8

C．74.2

D．113.0

问题背景 某课外学习小组在一次学习研讨中，得到如下两个命题：
①  如图1，O是正三角形ABC的中心，∠MON分别与AB、BC交于点P,Q，若∠MON = 120°，则四边形OPBQ的面积等于三角形ABC面积的三分之一.
②  如图2，O是正方形ABCD的中心，∠MON分别与AB、BC交于点P,Q，若∠MON = 90°，则四边形OPBQ的面积等于正方形ABCD面积的四分之一.然后运用类比的思想提出了如下的命题：
③  如图3，O是正五边形ABCDE的中心，∠MON分别与AB、BC交于点P,Q，若∠MON = 72°，则四边形OPBQ的面积等于五边形ABCDE面积的五分之一.
、任务要求 
（1）请你从①、②、③三个命题中选择一个进行证明；（说明：选①做对的得5分，选②做对的得4分，选③做对的得6分）
（2）请你继续完成下面的探索：
如图④，在正n（n≥3）边形ABCDEF…中，O是中心,∠MON分别与AB、BC交于点P,Q，若∠MON等于多少度时，则四边形OPBQ的面积等于正n边形ABCDE…面积的n分之一？（不要求证明）
解：（1）我选            .
证明：