如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,分别交BC,AD于E,F两点,交BA的延长于G,判断弧EF和弧FG是否相等,并说明理由。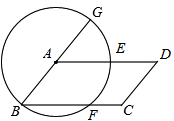
已知:如图,A、B、C为⊙O上的三个点,⊙O的直径为4cm,∠ACB=45°,求AB的长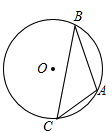
小明四等分弧AB,他的作法如下:
(1)连接AB(如图);
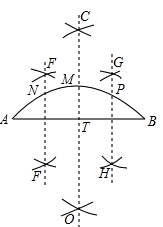
(2)作AB的垂直平分线CD交弧AB于点M,交AB于点T;
(3)分别作AT,TB的垂直平分线EF,GH,交弧AB于N,P两点,则N,M,P三点把弧AB四等分。你认为小明的作法是否正确: 理由是
如图1,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发沿图中某一个扇形顺时针匀速运动,设∠APB=y(单位:度),如果y与P运动的时间x(单位:秒),的函数关系的图象大致如图2所示,那么P的运动路线可能为( )

A.O→B→A→O B.O→A→C→O C.O→C→D→O D.O→B→D→O
如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于点C,连接BC,如果∠A=30°,AB=2 ,那么AC的长等于( )
,那么AC的长等于( )

| A.4 | B.6 | C.4 |
D.6 |
如果弧长为6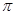 的弧所对的圆心角为60°,那么这条弧所在的圆的半径是( )
的弧所对的圆心角为60°,那么这条弧所在的圆的半径是( )
| A.18 | B.12 | C.36 | D.6 |
如图,⊙O的半径为5,AB为弦,OC⊥AB,垂足为C,如果OC=3,那么弦AB的长为( )

| A.4 | B.6 | C.8 | D.10 |
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.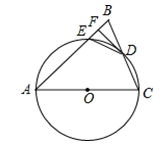
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
【发现】如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)
【思考】
如图②,如果∠ACB=∠ADB=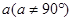 (点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?
(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?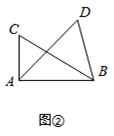
【证明】
经过一番思考,小明同学认为,若要证明点D仍然在经过A,B,C三点的圆上,只要证明出,点D既不在该圆外,也不在该圆内,即可得出点D还在经过A,B,C三点的圆上的结论.
小明同学证明出了点D不在圆外:
请你根据上述过程,画出图形,并证明点D也不在圆内.
如图,AB是⊙O的直径,点F,C是⊙O上两点,且F,C,B三等分半圆,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2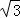 ,求⊙O的半径.
,求⊙O的半径.
如图,AB是⊙O的直径,CD为⊙O的弦,已知AB⊥CD,垂足为E,点M在⊙O上,MD恰好经过圆心O,连接MB.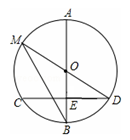
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.
如图所示,正方形网格中,每个小正方形的边长为1个单位,以O为原点建立平面直角坐标系.圆心为A(3,0)的A被y轴截得的弦长BC=8.解答下列问题:

(1)⊙A的半径为 ;
(2)若将⊙A先向上平移2个单位,再向右平移3个单位得到⊙D,则⊙D的圆心D点的坐标是 ;⊙D与x轴的位置关系是 ;⊙D与y轴的位置关系是 ;
(3)若将⊙A沿着水平方向平移 个单位长度,⊙A即可与y轴相切.
如图,要拧开一个边长为 的正六边形螺帽,扳手张开的开口
的正六边形螺帽,扳手张开的开口 至少为( )
至少为( )

A. |
B. |
C. |
D. |
将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上,点A、B的读数分别为86°、30°,则∠ACB的大小为( )

A.15° B.28° C.29° D.34°
试题篮
()