设 和 是两个等差数列,记 ,其中 表示 , …, 这s个数中最大的数.
(1)若 , ,求 , , 的值,并证明{cn}是等差数列;
(2)证明:或者对任意正数 ,存在正整数 ,当 时, ;或者存在正整数 ,使得 , , , …是等差数列.
给定无穷数列 ,若无穷数列{b n}满足:对任意 ,都有 ,则称 "接近"。
(1)设 是首项为1,公比为 的等比数列, , ,判断数列 是否与 接近,并说明理由;
(2)设数列 的前四项为: =1, =2, =4, =8, 是一个与 接近的数列,记集合M={x|x=b i, i=1,2,3,4},求M中元素的个数m;
(3)已知 是公差为d的等差数列,若存在数列{b n}满足:{b n}与 接近,且在b₂-b₁,b₃-b₂,…b 201-b 200中至少有100个为正数,求d的取值范围。
对于数列 若存在常数M>0,对任意的 ,恒有 则称数列 为B-数列
(1)首项为1,公比为 的等比数列是否为B-数列?请说明理由;
请以其中一组的一个论断条件,另一组中的一个论断为结论组成一个命题
判断所给命题的真假,并证明你的结论;
(2)设 是数列 的前 项和,给出下列两组论断;
A组:①数列 是B-数列 ②数列 不是B-数列
B组:③数列 是B-数列 ④数列 不是B-数列
请以其中一组中的一个论断为条件,另一组中的一个论断为结论组成一个命题。
判断所给命题的真假,并证明你的结论;
(3)若数列 都是 数列,证明:数列 也是 数列。
设函数 ,其中 。
(1)求 的单调区间;
(2)若 存在极点 , 且 ,其中 , 求证: ;
(3)设 ,函数 ,求证: 在区间 上的最大值不小于 .
已知 是各项均为整数得等差数列,公差为d,对任意的 , 是 和 得等比中项。
(1)设 , ,求证:数列 是等差数列;
(2)设 , , ,求证:
已知,椭圆C以过点, ,两个焦点为 。
(Ⅰ)求椭圆C的方程;
(Ⅱ)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
(1)已知矩阵 所对应的线性变换把点 变成点 ,试求M的逆矩阵及点A的坐标
(2)已知直线 与 试判断他们的公共点个数
(3)解不等式 .
已知曲线 .从点 向曲线 引斜率为 的切线 ,切点为 .
(1)求数列 的通项公式;
(2)证明:
已知抛物线 上一点 到其焦点的距离为 .
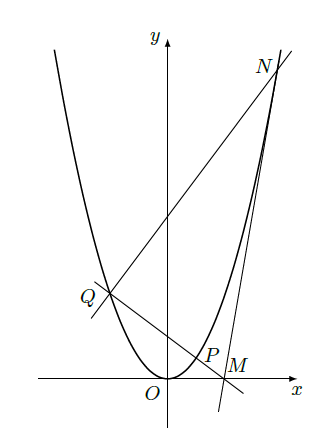
(Ⅰ)求 p于 m的值;
(Ⅱ)设抛物线C上一点 p的横坐标为 t( t>0),过 p的直线交C于另一点 Q,交 x轴于 M点,过点 Q作 PQ的垂线交 C于另一点 N.若 MN是 C的切线,求 t的最小值;
已知数集 具有性质 ;对任意的 , 与 两数中至少有一个属于 。
(Ⅰ)分别判断数集 与 是否具有性质 ,并说明理由;
(Ⅱ)证明: ,且
(Ⅲ)证明:当 时, 成等比数列。
设各项均为正数的数列 满足 .
(Ⅰ)若 求 , ,并猜想 的值(不需证明);
(Ⅱ)若 对 恒成立,求 的值.
已知函数 .
( I ) 求函数 的单调区间;
( II ) 若不等式 对任意的 都成立(其中 是自然对数的底数).求 的最大值.
试题篮
()