已知椭圆 的离心率为
的离心率为 ,以原点
,以原点 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线 相切。
相切。
(1)求椭圆 的标准方程;
的标准方程;
(2)若直线 与椭圆
与椭圆 相交于
相交于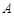 、
、 两点,且
两点,且 ,试判断
,试判断 的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
我们把一系列向量 排成一列,称为向量列,记作
排成一列,称为向量列,记作 ,又设
,又设 ,假设向量列
,假设向量列 满足:
满足: ,
, 。
。
(1)证明数列 是等比数列;
是等比数列;
(2)设 表示向量
表示向量 间的夹角,若
间的夹角,若 ,记
,记 的前
的前 项和为
项和为 ,求
,求 ;
;
(3)设 是
是 上不恒为零的函数,且对任意的
上不恒为零的函数,且对任意的 ,都有
,都有 ,若
,若 ,
, ,求数列
,求数列 的前
的前 项和
项和 .
.
在长方体ABCD—A1B1C1D1中, ,点E是棱AB上一点.且
,点E是棱AB上一点.且 .
.
(1)证明: ;
;
(2)若二面角D1—EC—D的大小为 ,求
,求 的值.
的值.
设数列{an}的首项不为零,前n项和为Sn,且对任意的r,t N*,都有
N*,都有 .
.
(1)求数列{an}的通项公式(用a1表示);
(2)设a1=1,b1=3, ,求证:数列
,求证:数列 为等比数列;
为等比数列;
(3)在(2)的条件下,求 .
.
在平面直角坐标系xOy中,设曲线C1: 所围成的封闭图形的面积为
所围成的封闭图形的面积为 ,曲线C1上的点到原点O的最短距离为
,曲线C1上的点到原点O的最短距离为 .以曲线C1与坐标轴的交点为顶点的椭圆记为C2.
.以曲线C1与坐标轴的交点为顶点的椭圆记为C2.
(1)求椭圆C2的标准方程;
(2)设AB是过椭圆C2中心O的任意弦,l是线段AB的垂直平分线.M是l上的点(与O不重合).
①若MO=2OA,当点A在椭圆C2上运动时,求点M的轨迹方程;
②若M是l与椭圆C2的交点,求△AMB的面积的最小值.
已知函数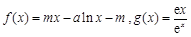 ,其中m,a均为实数.
,其中m,a均为实数.
(1)求 的极值;
的极值;
(2)设 ,若对任意的
,若对任意的
 ,
, 恒成立,求
恒成立,求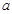 的最小值;
的最小值;
(3)设 ,若对任意给定的
,若对任意给定的 ,在区间
,在区间 上总存在
上总存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
如图,在平面直角坐标系 中,已知
中,已知 ,
, ,
, 是椭圆
是椭圆 上不同的三点,
上不同的三点, ,
, ,
, 在第三象限,线段
在第三象限,线段 的中点在直线
的中点在直线 上.
上.
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点 在椭圆上(异于点
在椭圆上(异于点 ,
, ,
, )且直线PB,PC分别交直线OA于
)且直线PB,PC分别交直线OA于 ,
, 两点,证明
两点,证明 为定值并求出该定值.
为定值并求出该定值.
已知函数 ,其中m,a均为实数.
,其中m,a均为实数.
(1)求 的极值;
的极值;
(2)设 ,若对任意的
,若对任意的
 ,
, 恒成立,求
恒成立,求 的最小值;
的最小值;
(3)设 ,若对任意给定的
,若对任意给定的 ,在区间
,在区间 上总存在
上总存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
如图,在平面直角坐标系 中,已知
中,已知 ,
, ,
, 是椭圆
是椭圆 上不同的三点,
上不同的三点, ,
, ,
, 在第三象限,线段
在第三象限,线段 的中点在直线
的中点在直线 上.
上.
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点 在椭圆上(异于点
在椭圆上(异于点 ,
, ,
, )且直线PB,PC分别交直线OA于
)且直线PB,PC分别交直线OA于 ,
, 两点,证明
两点,证明 为定值并求出该定值.
为定值并求出该定值.
已知函数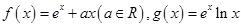 (e为自然对数的底数).
(e为自然对数的底数).
(1)设曲线 处的切线为
处的切线为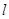 ,若
,若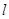 与点(1,0)的距离为
与点(1,0)的距离为 ,求a的值;
,求a的值;
(2)若对于任意实数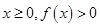 恒成立,试确定
恒成立,试确定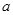 的取值范围;
的取值范围;
(3)当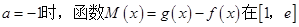 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
如图,椭圆的右焦点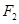 与抛物线
与抛物线 的焦点重合,过
的焦点重合,过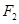 且于x轴垂直的直线与椭圆交于S,T,与抛物线交于C,D两点,且
且于x轴垂直的直线与椭圆交于S,T,与抛物线交于C,D两点,且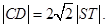

(1)求椭圆的标准方程;
(2)设P为椭圆上一点,若过点M(2,0)的直线 与椭圆相交于不同两点A和B,且满足
与椭圆相交于不同两点A和B,且满足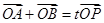 (O为坐标原点),求实数t的取值范围.
(O为坐标原点),求实数t的取值范围.
已知函数 ..
..
(1)设曲线 处的切线为
处的切线为 ,点(1,0)到直线l的距离为
,点(1,0)到直线l的距离为 ,求a的值;
,求a的值;
(2)若对于任意实数 恒成立,试确定
恒成立,试确定 的取值范围;
的取值范围;
(3)当 是否存在实数
是否存在实数 处的切线与y轴垂直?若存在,求出
处的切线与y轴垂直?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
设函数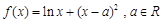
(1)若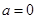 ,求函数
,求函数 在
在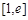 上的最小值;
上的最小值;
(2)若函数 在
在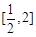 存在单调递增区间,试求实数
存在单调递增区间,试求实数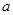 的取值范围;
的取值范围;
(3)求函数 的极值点.
的极值点.
已知椭圆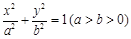 的右焦点为F,A为短轴的一个端点,且
的右焦点为F,A为短轴的一个端点,且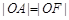 ,
,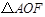 的面积为1(其中
的面积为1(其中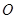 为坐标原点).
为坐标原点).
(1)求椭圆的方程;
(2)若C、D分别是椭圆长轴的左、右端点,动点M满足 ,连结CM,交椭圆于点
,连结CM,交椭圆于点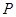 ,证明:
,证明: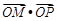 为定值;
为定值;
(3)在(2)的条件下,试问 轴上是否存在异于点C的定点Q,使得以MP为直径的圆恒过直线DP、MQ的交点,若存在,求出点Q的坐标;若不存在,说明理由.
轴上是否存在异于点C的定点Q,使得以MP为直径的圆恒过直线DP、MQ的交点,若存在,求出点Q的坐标;若不存在,说明理由.
试题篮
()