两个变量x,y与其线性相关系数r有下列说法
(1)若r>0,则x增大时,y也相应增大;
(2)若|r|越趋近于1,则x, y线性相关程度越强;
(3)若r=1或r=-1,则x与y的关系完全对应(有函数关系),在散点图上各个散点均在一条直线上,其中正确的有( )
| A.①② | B.②③ | C.①③ | D.①②③ |
下表为某公司员工连续加班时间与制造产品的几组数据,根据表中提供的数据,求出y关于 的线性回归方程为
的线性回归方程为 ,则表中t的值为 .
,则表中t的值为 .
 |
3 |
4 |
5 |
6 |
 |
2.5 |
t |
4 |
4.5 |
对变量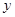 与
与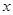 ,分别选择了4个不同的回归方程甲、乙、丙、丁,它们的相关系数
,分别选择了4个不同的回归方程甲、乙、丙、丁,它们的相关系数 分别为:
分别为:  ,
,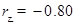 ,
, 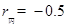 ,
,  . 其中拟合效果最好的是方程( ).
. 其中拟合效果最好的是方程( ).
| A.甲 | B.乙 | C.丙 | D.丁 |
某产品的广告费用x与销售额y的统计数据如表,根据此表可得回归方程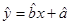 中的
中的 为9.4,据此模型预报广告费用为6万元时销售额为
为9.4,据此模型预报广告费用为6万元时销售额为
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
54 |
对于线性相关系数 ,叙述正确的是
,叙述正确的是
A.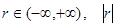 越大,相关程度越大,反之相关程度越小 越大,相关程度越大,反之相关程度越小 |
B.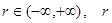 越大,相关程度越大,反之相关程度越小 越大,相关程度越大,反之相关程度越小 |
C.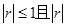 越接近1,相关程度越大 越接近1,相关程度越大 |
| D.以上说法都不对 |
对两个变量 和
和 进行回归分析,得到一组样本数据:
进行回归分析,得到一组样本数据: ,则下列说法中不正确的是( )
,则下列说法中不正确的是( )
A.由样本数据得到的回归方程 必过样本中心 必过样本中心 |
| B.残差平方和越小的模型,拟合的效果越好 |
C.用相关指数 来刻画回归效果, 来刻画回归效果, 越小,说明模型的似合效果越好 越小,说明模型的似合效果越好 |
D.若变量y和x之间的相关系数为 ,则变量y和x之间具有线性相关关系 ,则变量y和x之间具有线性相关关系 |
以下有关线性回归分析的说法不正确的是( )
A.通过最小二乘法得到的线性回归直线经过样本的中心 |
B.用最小二乘法求回归直线方程,是寻求使 最小的a,b的值 最小的a,b的值 |
| C.在回归分析中,变量间的关系若是非确定性关系,但因变量也能由自变量唯一确定 |
| D.如果回归系数是负的,y的值随x的增大而减小 |
两个变量 与
与 的回归模型中,分别选择了4个不同模型,它们的相关指数
的回归模型中,分别选择了4个不同模型,它们的相关指数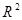 如下 ,其中拟合效果最好的模型是( )
如下 ,其中拟合效果最好的模型是( )
A.模型1的相关指数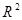 为0.98 为0.98 |
B.模型2的相关指数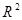 为0.80 为0.80 |
C.模型3的相关指数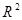 为0.50 为0.50 |
D.模型4的相关指数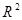 为0.25 为0.25 |
下面是2×2 列联表
| x y |
y 1 |
y 2 |
合计 |
| x1 |
a |
21 |
73 |
| x2 |
2 |
25 |
27 |
| 合计 |
b |
46 |
100 |
则表中 a 、b 处的值分别为( )
A.94 、96 B.52 、50 C.52 、54 D.54 、52
为了解儿子身高与其父亲身高的关系,随机抽取5对父子身高数据如下
| 父亲身高x(cm) |
174 |
176 |
176 |
176 |
178 |
| 儿子身高y(cm) |
175 |
175 |
176 |
177 |
177 |
则y对x的线性回归方程为 ( )
A. B.
B.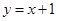 C.
C. D.
D.
已知x与y之间的一组数据:
| x |
0 |
1 |
2 |
3 |
| y |
1 |
3 |
5 |
7 |
则y与x的线性回归方程为y=bx+a必过点__________________________.
某中学共2200名学生中有男生1200名,按男女性别用分层抽样抽出110名学生,询问是否爱好某项运动。已知男生中有40名爱好该项运动,女生中有30名不爱好该项运动。
(1)如下的列联表:
| |
男 |
女 |
总计 |
| 爱好 |
40 |
|
|
| 不爱好 |
|
30 |
|
| 总计 |
|
|
|
(2)通过计算说明,是否有99%以上的把握认为“爱好该项运动与性别有关”? 参考信息如下:
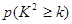 |
0.050 |
0.010 |
0.001 |
| k |
3.841 |
6.635 |
10.828 |
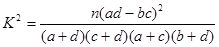
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100棵种子中的发芽数,得到如下资料:
| 日期 |
12月1日 |
12月2日 |
12月3日 |
12月4日 |
12月5日 |
| 温差x(℃) |
10 |
11 |
13 |
12 |
8 |
| 发芽y(颗) |
23 |
25 |
30 |
26 |
16 |
该农科所确定的研究方案是:先从这5组数据中选取3组数据求线性回归方程,剩下的2组数据用于回归方程检验.
回归直线方程参考公式:
 ,
, 

(1)请根据12月2日至12月4日的数据,求出y关于x的线性回归方程 ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则
认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(3)请预测温差为14℃的发芽数。
试题篮
()