设某大学的女生体重 (单位:
(单位: )与身高
)与身高 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据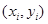 (
( ),用最小二乘法建立的回归方程为
),用最小二乘法建立的回归方程为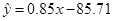 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心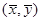 |
C.若该大学某女生身高增加 ,则其体重约增加 ,则其体重约增加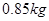 |
D.若该大学某女生身高为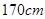 ,则可断定其体重为 ,则可断定其体重为 |
对具有线性相关关系的变量 和
和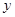 ,测得一组数据如下:
,测得一组数据如下:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
若已求得它们的回归方程的斜率为6.5,则这条直线的回归方程为 .
从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
身高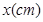 |
160 |
165 |
170 |
175 |
180 |
体重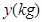 |
63 |
66 |
70 |
72 |
74 |
根据上表可得回归直线方程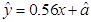 ,据此模型预报身高为172
,据此模型预报身高为172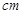 的高三男生的体重为 ( )
的高三男生的体重为 ( )
A.70.09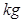 B.70.12
B.70.12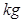 C.70.55
C.70.55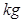 D.71.05
D.71.05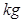
设有一个回归直线方程为 ,则变量x增加一个单位时
,则变量x增加一个单位时
| A.y平均增加1.5个单位 | B.y平均增加2个单位 |
| C.y平均减少1.5个单位 | D.y平均减少2个单位 |
已知某回归直线过点 ,且样本数据中
,且样本数据中 和
和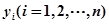 的均值分别为
的均值分别为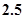 和
和 ,则此回归直线方程为 .
,则此回归直线方程为 .
调查某市出租车使用年限 和该年支出维修费用
和该年支出维修费用 (万元),得到数据如下:
(万元),得到数据如下:
使用年限 |
2 |
3 |
4 |
5 |
6 |
维修费用 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
则回归方程 ,必过定点
,必过定点
A.(2,3) B.(3,4) C.(4,5) D.(5,6)
下表是某厂1—4月份用水量(单位:百吨)的一组数据:
| 月份x |
1 |
2 |
3 |
4 |
| 用水量y |
4.5 |
4 |
3 |
2.5 |
由散点图可知,用水量与月份之间有较好的线性相关关系,其线性回归方程为 =-0.7x+a,则a等于( )
=-0.7x+a,则a等于( )
A.10.5 B.5.15 C.5.2 D.5.25
下列说法中正确的有( )
①若r>0,则x增大时,y也相应增大; ②若r<0,则x增大时,y也相应增大;
③若r=1或r=-1,则x与y的关系完全对应(有函数关系),在散点图上各个点均在一条直线上.
| A.①② | B.②③ | C.①③ | D.①②③ |
在一次独立性检验中,有300人按性别和是否色弱分类如下表:
| |
男 |
女 |
| 正常 |
130 |
120 |
| 色弱 |
20 |
30 |
由此表计算得统计量K2=( ).
(参考公式: )
)
A.2 B.3 C.2.4 D.3.6
某工厂经过技术改造后,降低了能源消耗,经统计该厂某种产品的产量x(单位:吨)与相应的生产能耗y(单位:吨)有如下几组样本数据:
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
根据相关性检验,这组样本数据具有线性相关关系,通过线性回归分析,求得回归直线的斜率为0.7.已知该产品的年产量为10吨,则该工厂每年大约消耗的汽油为________吨.
试题篮
()