如图是某居民小区年龄在20岁到45岁的居民上网情况的频率分布直方图,现已知年龄 在[30,35),[35,40),[40,45]的上网人数呈现递减的等差数列,则年龄在[35,40)的频率( )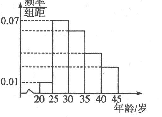
| A.0.04 |
| B.0.06 |
| C.0.2 |
| D.0.3 |
从某学校的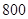 名男生中随机抽取
名男生中随机抽取 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于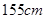 和
和 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组 ,第二组
,第二组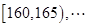 ,第八组
,第八组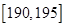 ,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为 人。
人。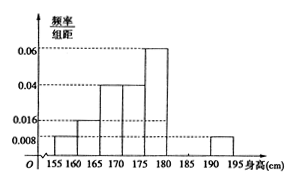
(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的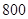 名男生的身高的中位数以及身高在
名男生的身高的中位数以及身高在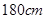 以上(含
以上(含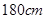 )的人数;
)的人数;
(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 ,事件
,事件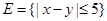 ,事件
,事件 ,求
,求
将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场作的9个分数的茎叶图,后来有1个数据模糊,无法辨认,在图中以x表示,则7个剩余分数的方差为( )
A. |
B. |
C.36 | D.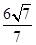 |
某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量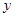 (单位:微克)与时间
(单位:微克)与时间 (单位:小时)之间近似满足如图所示的曲线,
(单位:小时)之间近似满足如图所示的曲线,
(1)写出第一次服药后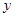 与
与 之间的函数关系式;
之间的函数关系式;
(2)据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到
微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到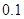 ,参考数据:
,参考数据: )
)
某产品的广告费用x与销售额y的统计数据如下表:
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
54 |
根据上表可得回归方程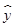 =
=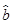 x+
x+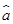 中的
中的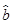 为9.4,据此模型预报广告费用为6万元时销售额为( )
为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元 B.65.5万元 C.67.7万元 D.72.0万元
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗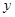 (吨标准煤)的几组对应数据﹒
(吨标准煤)的几组对应数据﹒
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
m |
4 |
4.5 |
根据上表提供的数据,求出y关于x的线性回归方程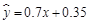 ,那么表中m的值为 .
,那么表中m的值为 .
从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:由下表可得回归直线方程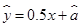 ,据此模型预报身高为
,据此模型预报身高为 的男生的体重大约为( )
的男生的体重大约为( )
身高 |
160 |
165 |
170 |
175 |
180 |
体重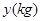 |
63 |
66 |
70 |
72 |
74 |
A.69.5 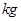 B.70
B.70 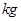 C.70.5
C.70.5 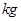 D.71
D.71 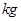
下面四个命题中真命题的是( )
①从匀速传递的产品生产流水线上,质检员每15分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②两个随机变量相关性越强,则相关系数的绝对值越接近于1;
③在回归直线方程 =0.4x+12中,当解释变量x每增加一个单位时,预报变量平均增加0.4个单位;
=0.4x+12中,当解释变量x每增加一个单位时,预报变量平均增加0.4个单位;
④对分类变量X与Y的随机变量K2的观测值k来说,k越小,“X与Y有关系”的把握程度越大.
| A.①④ | B.②④ | C.①③ | D.②③ |
根据如下样本数据
| x |
3 |
4 |
5 |
6 |
7 |
| y |
4.0 |
2.5 |
 0.5 0.5 |
0.5 |
 2.0 2.0 |
得到的回归方程为 .若
.若 ,则
,则 的值为
的值为
A. B.
B. C.
C. D.
D.
根据如下样本数据:
| x |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
4 |
2.5 |
 |
0.5 |
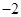 |
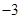 |
| x |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
4 |
2.5 |
-0.5 |
0.5 |
-2 |
-3 |
得到的回归方程为 ,则( )
,则( )
A.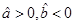 B.
B.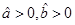
C.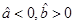 D.
D.
已知变量x与y正相关,且由观测数据算得样本平均数线性回归方程 =3,
=3, =3.5,则由
=3.5,则由
该观测数据算得的线性回归方程可能是( )
A. =-2x+9.5 =-2x+9.5 |
B. =2x-2.4 =2x-2.4 |
C. =0.4x+2.3 =0.4x+2.3 |
D. =-0.3x+4.4 =-0.3x+4.4 |
某商场在今年端午节的促销活动中,对6月2日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额为( )
| A.8万元 | B.10万元 |
| C.12万元 | D.15万元 |
试题篮
()