某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据:由资料显示 对
对 呈线性相关关系。
呈线性相关关系。
根据上表提供的数据得到回归方程 中的
中的 ,预测销售额为115万元时约需
,预测销售额为115万元时约需
万元广告费.
某校的研究性学习小组为了研究中学生的身高与性别情况,在该校随机抽出80名17至18周岁的学生,其中身高 的男生有30人,女生4人;身高<170的男生有10人。
的男生有30人,女生4人;身高<170的男生有10人。
(1)根据以上数据建立一个 列联表:
列联表:
(2)请问在犯错误的概率不超过0.001的前提下,该校17至18周岁的学生的身高与性别是否有关?
参考公式: 
参考数据: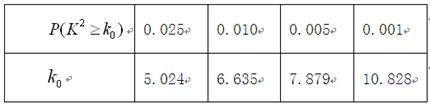
.对相关系数r,下列说法正确的是 ( )
A. 越大,线性相关程度越大 越大,线性相关程度越大 |
B. 越小,线性相关程度越大 越小,线性相关程度越大 |
C. 越大,线性相关程度越小, 越大,线性相关程度越小, 越接近0,线性相关程度越大 越接近0,线性相关程度越大 |
D. 且 且 越接近1,线性相关程度越大, 越接近1,线性相关程度越大, 越接近0,线性相关程度越小 越接近0,线性相关程度越小 |
已知有线性相关关系的两个变量建立的回归直线方程为 ,方程中的回归系数
,方程中的回归系数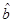 ( )
( )
| A.可以小于0 | B.只能大于0 | C.可以为0 | D.只能小于0 |
对某市工薪阶层关于“楼市限购政策”的态度进行调查,随机抽查了50人,他们月收入(单位:百元)的频数分布及对“楼市限购政策”赞成人数如下表:
| 月收入(单位百元) |
[15,25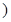 |
[25,35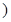 |
[35,45 |
[45,55 |
[55,65 |
[65,75 |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(Ⅰ)根据以上统计数据填写下面2×2列联表,并回答是否有99%的把握认为月收入以5500元为分界点对“楼市限购政策” 的态度有差异?
| |
月收入不低于55百元的人数 |
月收入低于55百元的人数 |
合计 |
| 赞成 |
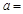 3 3 |
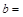 |
|
| 不赞成 |
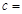 |
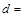 11 11 |
|
| 合计 |
|
|
50 |
(Ⅱ)若从月收入在[55,65)的被调查对象中随机选取两人进行调查,求至少有一人赞成“楼市限购政策”的概率.
(参考公式: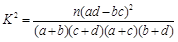 ,其中
,其中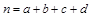 .)
.)
参考值表:
P(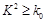 ) ) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
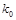 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程 =0.7x+0.35,那么表中m的值为( )
=0.7x+0.35,那么表中m的值为( )
| A.4 | B.3.15 | C.4.5 | D.3 |
调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程: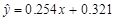 .由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加____________万元.
.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加____________万元.
某产品的广告费用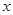 与销售额
与销售额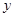 的统计数据如下表:
的统计数据如下表:
广告费用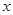 (万元) (万元) |
4 |
2 |
3 |
5 |
销售额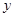 (万元) (万元) |
49 |
26 |
39 |
54 |
根据上表数据预计广告费用为6万元时,销售额为( )
A.63.6万元 B.65.5万元 C.67.7万元 D.72.0万元
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
| 转速x(转/秒) |
2 |
4 |
5 |
6 |
8 |
| 每小时生产有缺点的零件数y(件) |
30 |
40 |
60 |
50 |
70 |
(1)画散点图
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为89个,那么机器的运转速度应控制在什么范围内?(参考数值: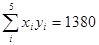 ,
, )
)
在两个变量 与
与 的回归模型中,分别选择了4个不同的模型,它们的相关指数R2如下,其中拟合效果最好的模型是
的回归模型中,分别选择了4个不同的模型,它们的相关指数R2如下,其中拟合效果最好的模型是
| A.模型1的相关指数R2为0.98 | B.模型2的相关指数R2为0.90 |
| C.模型3的相关指数R2为0.60 | D.模型4的相关指数R2为0.25 |
甲乙两个学校高三年级分别有1100人和1000人,为了了解这两个学校全体高三年级学生在该地区二模考试中的数学成绩情况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了如下的频数分布统汁表,规定考试成绩在[120,150]内为优秀.
(I)试求x,y的值;
(II)由以上统计数据填写右面2×2列联表,若按是否优秀来判断,是否有97.5%的把握
认为两个学校的数学成绩有差异。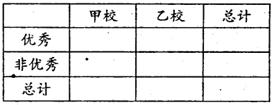
(III)根据抽样结果分别估计甲校和乙校的优秀率,若把频率视为概率,现从乙校学生中任取3人,求优秀学生人数ξ的分布列和数学期望。
附:
下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程 =0.7x+0.35,那么表中m的值为( )
=0.7x+0.35,那么表中m的值为( )
| A.4 | B.3.15 | C.4.5 | D.3 |
(本小题满分12分)为了分析某个高中学生的学习状态,对其下一阶段的学习提供指导性建议。现对他前7次考试的数学成绩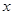 、物理成绩
、物理成绩 进行分析。下面是该生7次考试的成绩,可见该生的物理成绩
进行分析。下面是该生7次考试的成绩,可见该生的物理成绩 与数学成绩
与数学成绩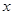 是线性相关的:
是线性相关的:
| 数学 |
88 |
83 |
117 |
92 |
108 |
100 |
112 |
| 物理 |
94 |
91 |
108 |
96 |
104 |
101 |
106 |
(1)求物理成绩 与数学成绩
与数学成绩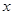 的回归直线方程
的回归直线方程 ;
;
(2)若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?
参考公式: ,
, 
参考数据: ,
,
试题篮
()