下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 =bx+a.
=bx+a.
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
某班主任对全班50名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有18人,认为作业不多的有9人,不喜欢玩电脑游戏的同学认为作业多的有8人,认为作业不多的有15人.
(1)根据以上数据建立一个2×2的列联表.
(2)有多大的把握认为“喜欢玩电脑游戏与认为作业多有关系”?
(参考数值: ≈5.059)
≈5.059)
某地粮食需求量逐年上升,下表是部分统计数据:
| 年份(年) |
2002 |
2004 |
2006 |
2008 |
2010 |
| 需求量 (万吨) |
236 |
246 |
257 |
276 |
286 |
(1)利用所给数据求年需求量与年份之间的回归直线方程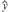 =
= x+
x+ .
.
(2)利用(1)中所求出的直线方程预测该地2014年的粮食需求量.
一家商场为了确定营销策略,进行了投入促销费用x和商场实际销售额y的试验,得到如下四组数据.
| 投入促销费用x(万元) |
2 |
3 |
5 |
6 |
| 商场实际营销额y(万元) |
100 |
200 |
300 |
400 |
(1)在下面的直角坐标系中,画出上述数据的散点图,并据此判断两个变量是否具有较好的线性相关性;
(2)求出x,y之间的回归直线方程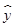 =
=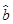 x+
x+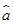 ;
;
(3)若该商场计划营销额不低于600万元,则至少要投入多少万元的促销费用?
2013年4月14日,CCTV财经频道报道了某地建筑市场存在违规使用未经淡化海砂的现象.为了研究使用淡化海砂与混凝土耐久性是否达标有关,某大学实验室随机抽取了60个样本,得到了相关数据如下表:
| |
混凝土耐久性达标 |
混凝土耐久性不达标 |
总计 |
| 使用淡化海砂 |
25 |
 |
30 |
| 使用未经淡化海砂 |
 |
15 |
30 |
| 总计 |
40 |
20 |
60 |
(Ⅰ)根据表中数据,求出 ,
, 的值,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关?
的值,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关?
(Ⅱ)若用分层抽样的方法在使用淡化海砂的样本中抽取了6个,现从这6个样本中任取2个,则取出的2个样本混凝土耐久性都达标的概率是多少?
参考数据:
 |
0.10 |
0.050 |
0.025 |
0.010 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
参考公式: 
某年青教师近五年内所带班级的数学平均成绩统计数据如下:
年份 年 年 |
2009 |
2010 |
2011 |
2012 |
2013 |
平均成绩 分 分 |
97 |
98 |
103 |
108 |
109 |
(1)利用所给数据,求出平均分与年份之间的回归直线方程 ,并判断它们之间是正相关还是负相关。
,并判断它们之间是正相关还是负相关。
(2)利用(1)中所求出的直线方程预测该教师2014年所带班级的数学平均成绩.



改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村2001到2005年五年间每年考入大学的人数,为了方便计算,2001年编号为1,2002年编号为2,……,2005年编号为5,数据如下:
| 年份(x) |
1 |
2 |
3 |
4 |
5 |
| 人数(y) |
3 |
5 |
8 |
11 |
13 |
(1)从这5年中随机抽取两年,求考入大学的人数至少有 年多于10人的概率.
年多于10人的概率.
(2)根据这 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出 关于
关于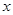 的回归方程
的回归方程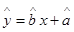 ,并计算第
,并计算第 年的估计值。
年的估计值。
参考:用最小二乘法求线性回归方程系数公式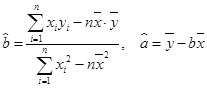
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村2001到2005年五年间每年考入大学的人数,为了方便计算,2001年编号为1,2002年编号为2,……,2005年编号为5,数据如下:
| 年份(x) |
1 |
2 |
3 |
4 |
5 |
| 人数(y) |
3 |
5 |
8 |
11 |
13 |
(1)从这5年中随机抽取两年,求考入大学的人数至少有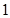 年多于10人的概率.
年多于10人的概率.
(2)根据这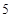 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出 关于
关于 的回归方程
的回归方程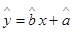 ,并计算第
,并计算第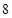 年的估计值。
年的估计值。
参考:用最小二乘法求线性回归方程系数公式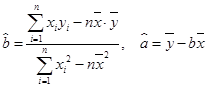
某种产品的广告费支出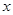 与销售额
与销售额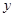 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
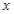 |
2 |
4 |
5 |
6 |
8 |
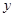 |
30 |
40 |
60 |
50 |
70 |
(1)求回归直线方程;
(2)试预测广告费支出为10万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
(参考数据:
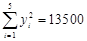
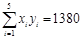
参考公式:线性回归方程系数: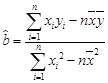 ,
, )
)
一次考试中,五名学生的数学、物理成绩如下表所示: 
(1)要从 5 名学生中选2 人参加一项活动,求选中的学生中至少有一人的物理成绩高于90分的概率;
(2)请在所给的直角坐标系中画出它们的散点图,并求这些数据的线性回归方程  .
.
(附:回归直线的方程是 :  , 其中
, 其中 )
)
为了调查胃病是否与生活规律有关,调查某地540名40岁以上的人得结果如下:
| |
患胃病 |
未患胃病 |
合计 |
| 生活不规律 |
60 |
260 |
320 |
| 生活有规律 |
20 |
200 |
220 |
| 合计 |
80 |
460 |
540 |
根据以上数据回答40岁以上的人患胃病与生活规律有关吗?
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据。
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)请根据上表提供的数据, y关于x的线性回归方程 ;
;
(2)已知该厂技改前100吨甲产品生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考公式: )
)
(本小题12分)下表提供了工厂技术改造后某种型号设备的使用年限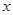 和所支出的维修费用
和所支出的维修费用 (万元)的几组对照数据:
(万元)的几组对照数据:
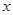 (年) (年) |
 |
 |
 |
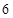 |
 (万元) (万元) |
 |
 |
 |
 |
(1)若知道 对
对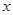 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出 关于
关于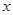 的线性回归方程
的线性回归方程 ;
;
(2)已知工厂技改前该型号设备使用10年的维修费用为9万元.试根据(1)求出的线性回归方程,预测该型号设备技改后使用10年的维修费用比技改前降低多少?
某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) |
2 |
3 |
4 |
5 |
| 加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1) 求出y关于x的线性回归方程;
(2) 试预测加工10个零件需要多少时间?
试题篮
()