为考察某种甲型H1N1疫苗的效果,进行动物实验,得到如下疫苗效果的实验列联表:
| |
感染 |
 未感染 未感染 |
总计 |
| 没服用 |
20 |
30 |
50 |
| 服用 |
x |
y |
50 |
| 总计 |
M |
N |
100 |
设从没服用疫苗的动物中任取两只,感染数为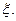 从服从过疫苗的动物中任取两只,感染数为
从服从过疫苗的动物中任取两只,感染数为 工作人员曾计算过
工作人员曾计算过
 (
( 1)求出列联表中数据
1)求出列联表中数据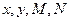 的值;
的值;
(2)写出 的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
(3)能够以97.5%的把握认为这种甲型H1N1疫苗有效么?并说明理由。
参考公式:
 参考数据:
参考数据:
 |
0.05 |
0.025 |
0.010 |
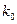 |
3.841 |
5.024 |
6.635 |
(本题满分12分)班主任为了对本班学生的考试成绩进行分析,决定从全班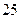 位女同学,
位女同学, 位男同学中随机抽取一个容量为
位男同学中随机抽取一个容量为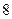 的样本进行分析。
的样本进行分析。
(Ⅰ)如果按性别比例分层抽样,可以得到多少个不同的样本(只要求写出算式即可,不必计算出结果);
(Ⅱ)随机抽取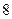 位同学,数学成绩由低到高依次为:
位同学,数学成绩由低到高依次为: ;
;
物理成绩由低到高依次为: ,若规定
,若规定 分(含
分(含 分)以
分)以 上为优秀,记
上为优秀,记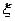 为这
为这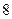 位同学中数学和物理分数均为优秀的人数,求
位同学中数学和物理分数均为优秀的人数,求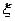 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)若这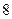 位同学的数学、物理分数事实上对应下表:
位同学的数学、物理分数事实上对应下表:
| 学生编号 |
 |
 |
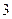 |
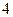 |
 |
 |
 |
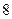 |
数学分数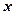 |
 |
 |
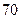 |
 |
 |
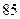 |
 |
 |
物理分数 |
 |
 |
 |
 |
 |
 |
 |
 |
根据上表数据可知,变量 与
与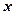
 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出 与
与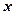 的线性回归方程(系数精确到
的线性回归方程(系数精确到 ).(参考公式:
).(参考公式: ,其中
,其中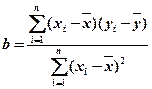 ,
, ; 参考数据:
; 参考数据: ,
, ,
, ,
, ,
, ,
,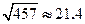 ,
, )
)
(本小题满分12分)
某公司近年来科研费用支出 万元与公司所获得利润
万元与公司所获得利润 万元之间有如下的统计数据:
万元之间有如下的统计数据:
 |
2 |
3 |
4 |
5 |
 |
18 |
27 |
32 |
35 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(3)试根据(2)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润.
参考公式:
为了分析某个高三学生的学习状态,对其下一阶段的学习作出预测和提供指导性建议,现对他前7次考试的数学成绩x、物理成绩y进行分析.下面是该生7次考试的成绩.
| 数学 |
88 |
83 |
117 |
92 |
108 |
100 |
112 |
| 物理 |
94 |
91 |
108 |
96 |
104 |
101 |
106 |
(1)分别求出这个考生的他的数学平均成绩与物理平均成绩,并判断在这个学科中哪科成绩更稳定;
(2)已知该生的物理成绩y与数学成绩x是线性相关的,求出线性回归方程;
(3)若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?
参考公式: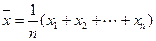 ,
,
(本小题满分12分)在调查的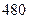 名上网的学生中有
名上网的学生中有 名学生睡眠不好,
名学生睡眠不好,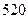 名不上网的学生中有
名不上网的学生中有 名学生睡眠不好,利用独立性检验的方法来判断是否能以
名学生睡眠不好,利用独立性检验的方法来判断是否能以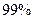 的把握认为“上网和睡眠是否有关系”.
的把握认为“上网和睡眠是否有关系”.
附: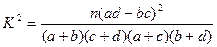 ;
;
参考数据
 |
 |
 |
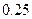 |
 |
 |
 |
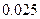 |
 |
 |
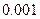 |
 |
 |
 |
 |
 |
 |
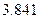 |
 |
 |
 |
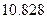 |
 ,
, .
.
(本小题满分12分)
某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示.
(Ⅰ)求甲、乙两名运动员得分的中位数;
(Ⅱ)你认为哪位运动员的成绩更稳定?
(Ⅲ)如果从甲、乙两位运动员的7场得分中各随机抽取一场的得分,求甲的得分大于乙的得分的概率.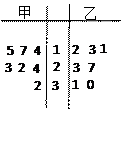
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
(Ⅰ)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(Ⅱ)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由.
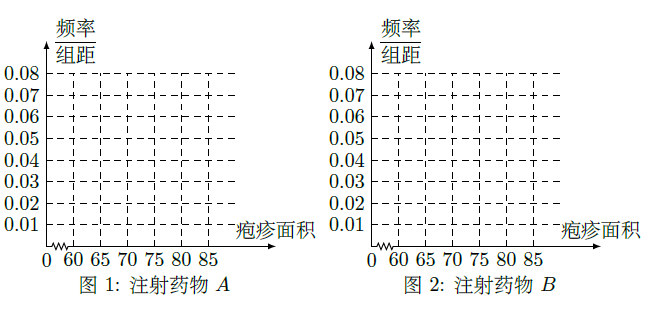
为了比较注射
两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随即地分成两组。每组100只,其中一组注射药物
,另一组注射药物
.下表1和表2分别是注射药物A和药物B后的实验结果。(疱疹面积单位:
)
表1:注射药物
后皮肤疱疹面积的频数分布表

表2:注射药物 后皮肤疱疹面积的频数分布表

(Ⅰ)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
(Ⅱ)完成下面
列联表,并回答能否有99.9%的把握认为"注射药物
后的疱疹面积与注射药物
后的疱疹面积有差异".
表3:

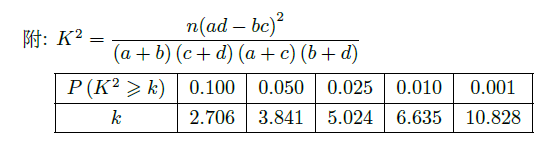
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老人,结果如下:
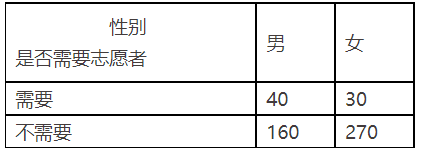
(Ⅰ)估计该地区老年人中,需要志愿提供帮助的老年人的比例;
(Ⅱ)能否有99℅的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的调查办法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由。
附:

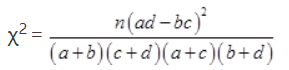
为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
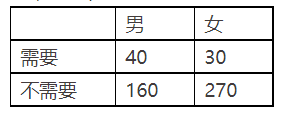
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有
的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提供更好的调查方法来估计该地区老年人,需要志愿帮助的老年人的比例?说明理由.
附:
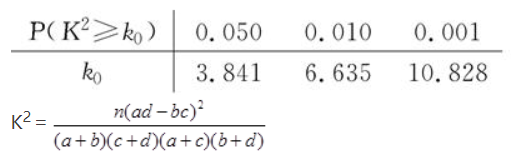
(本小题满分14分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
 |
3 |
4 |
5 |
6 |
 |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
17.(本小题满分13分)
汽车是碳排放量比较大的行业之一.欧盟规定,从2012年开始,将对 排放量超过
排放量超过 的
的 型新车进行惩罚.某检测单位对甲、乙两类
型新车进行惩罚.某检测单位对甲、乙两类 型品牌车各抽取
型品牌车各抽取 辆进行
辆进行 排放量检测,记录如下(单位:
排放量检测,记录如下(单位: ).
).
| 甲 |
80 |
110 |
120 |
140 |
150 |
| 乙 |
100 |
120 |
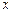 |
 |
160 |
经测算发现,乙品牌车 排放量的平均值为
排放量的平均值为
 .
.
(Ⅰ)从被检测的5辆甲类品牌车中任取2辆,则至少有一辆不符合 排放量的概率是多少?
排放量的概率是多少?
(Ⅱ)若 ,试比较甲、乙两类品牌车
,试比较甲、乙两类品牌车 排放量的稳定性.
排放量的稳定性.
测得某国家10对父子身高(单位:英寸)如下:
| 父亲身高(x) |
60 |
62 |
64 |
65 |
66 |
67 |
68 |
70 |
72 |
74 |
| 儿子身高(y) |
63.6 |
65.2 |
66 |
65.5 |
66.9 |
67.1 |
67.4 |
68.3 |
70.1 |
70 |
(1)对变量y与x进行相关性检验;
(2)如果y与x之间具有线性相关关系,求回归直线方程;
(3)如果父亲的身高为73英寸,估计儿子的身高.
某地10户家庭的年收入和年饮食支出的统计资料如下表:
| 年收入 x(万元) |
2 |
4 |
4 |
6 |
6 |
6 |
7 |
7 |
8 |
10 |
| 年饮食支出 y(万元) |
0.9 |
1.4 |
1.6 |
2.0 |
2.1 |
1.9 |
1.8 |
2.1 |
2.2 |
2.3 |
(1)根据表中数据,确定家庭的年收入和年饮食支出之间是否具有相关关系;若具有相关关系求出y与x的回归直线方程;
(2)如果某家庭年收入为9万元,预测其年饮食支出.
试题篮
()