如果随机变量ξ~B(n,p),且Eξ=7,Dξ=6,则P等于_________ .
有人收集了春节期间平均气温x(℃)与某取暖商品销售额y(万元)的有关数据(x,y)分别为:(﹣2,20),(﹣3,23),(﹣5,27),(﹣6,30),根据以上数据,用线性回归的方法,求得销售额y与平均气温x之间线性回归方程y=bx+a的系数b=﹣2.4,则预测平均气温为﹣8℃时该商品的销售额为_________ 万元.
下列五个命题
①任何两个变量都具有相关关系 ②圆的周长与该圆的半径具有相关关系
③某商品的需求量与该商品的价格是一种非确定性关系
④根据散点图求得的回归直线方程可能是没有意义的
⑤两个变量间的相关关系可以通过回归直线,把非确定性问题转化为确定性问题进行研究
正确命题的序号为____________.
[2013·怀柔模拟]某中学2013年共91人参加高考,统计数据如下:
| |
城镇考生 |
农村考生 |
| 录取 |
31 |
24 |
| 未录取 |
19 |
17 |
则考生的户口形式和高考录取的关系是________.(填无关、多大把握有关)
某班的全体学生参加消防安全知识竞赛,成绩的频率分布直方图如图,数据的分组依次为:
[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是 .
在2014年元旦期间,某市物价部门对本市五个商场销售的某商品一天的销售量及其价格进行调查,五个商场的售价x元和销售量y件之间的一组数据如表所示:
| 价格x |
9 |
9.5 |
10 |
10.5 |
11 |
| 销售量y |
11 |
10 |
8 |
6 |
5 |
通过分析,发现销售量y与商品的价格x具有线性相关关系,则销售量y关于商品的价格x的线性回归方程为__________.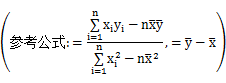
科研人员研究某物质的溶解度 与温度
与温度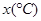 之间的关系,得到如下表部分数据,则其回归直线方程为 (
之间的关系,得到如下表部分数据,则其回归直线方程为 (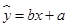 ,其中
,其中 ).
).
温度 (℃) (℃) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
溶解度 |
90 |
84 |
83 |
80 |
75 |
68 |
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下:
| 零件数x(个) |
10 |
20 |
30 |
40 |
50 |
| 加工时间y(分钟) |
64 |
69 |
75 |
82 |
90 |
由表中数据,求得线性回归方程 ,根据回归方程,预测加工70个零件所花费的时间为________分钟.
,根据回归方程,预测加工70个零件所花费的时间为________分钟.
在研究硝酸钠的可溶性程度时,对于不同的温度观测它在水中的溶解度,得观测结果如下:
| 温度(x) |
0 |
10 |
20 |
50 |
70 |
| 溶解度(y) |
66.7 |
76.0 |
85.0 |
112.3 |
128.0 |
由资料看y与x呈线性相关,试求线性回归方程为________.
由一组样本数据(x1,y1),(x2,y2),…,(xn,yn)得到线性回归方程 =
= x+
x+ ,那么下列说法正确的是________.
,那么下列说法正确的是________.
①直线 =
= x+
x+ 必经过点(
必经过点( ,
, );
);
②直线 =
= x+
x+ 至少经过点(x1,y1),(x2,y2),…,(xn,yn)中的一个点;
至少经过点(x1,y1),(x2,y2),…,(xn,yn)中的一个点;
③直线 =
= x+
x+ 的斜率为
的斜率为 ;
;
④直线 =
= x+
x+ 和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差
和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差 是该坐标平面上的直线与这些点的最小偏差.
是该坐标平面上的直线与这些点的最小偏差.
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为 =0.85x-85.71,给定下列结论:
=0.85x-85.71,给定下列结论:
①y与x具有正的线性相关关系;
②回归直线过样本点的中心(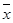 ,
, );
);
③若该大学某女生身高增加1cm,则其体重约增加0.85kg;
④若该大学某女生身高为170cm,则可断定其体重必为58.79kg.
其中正确的结论是 .
试题篮
()