观察图形规律,在其右下角的空格内画上合适的图形为( )
| A.▄ | B.△ | C. |
D.○ |
推理:“①矩形是平行四边形;②三角形不是平行四边形;③所以三角形不是矩形.”中的小前提是( )
| A.① | B.② | C.③ | D.①和② |
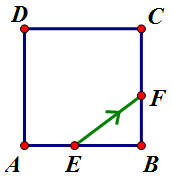
正方形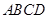 的边长为1,点
的边长为1,点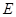 在边
在边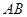 上,点
上,点 在边
在边 上,
上, ,动点
,动点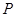 从
从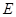 出发沿直线向
出发沿直线向 运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当点
运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当点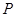 第一次碰到
第一次碰到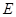 时,
时,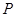 与正方形的边碰撞的次数为( )
与正方形的边碰撞的次数为( )
| A.16 | B.14 | C.12 | D.10 |
设数列{2n-1}按第n组有n个数(n是正整数)的规则分组如下:(1),(2,4),(8,16,32),…,则第101组中的第一个数为( )
| A.24 951 |
| B.24 950 |
| C.25 051 |
| D.25 050 |
一同学在电脑中打出如下若干个圆:○●○○●○○○●○○○○●○○○○○●…,若依此规律继续下去,得到一系列的圆,则在前2 012个圆中共有●的个数是( )
| A.61 | B.62 | C.63 | D.64 |
下列推理是归纳推理的是 ( )
A. 为定点,动点 为定点,动点 满足 满足  ,则动点 ,则动点 的轨迹是以 的轨迹是以 为焦点的双曲线; 为焦点的双曲线; |
B.由 求出 求出 猜想出数列 猜想出数列 的前 的前 项和 项和 的表达式; 的表达式; |
C.由圆 的面积 的面积 ,猜想出椭圆 ,猜想出椭圆 的面积 的面积 ; ; |
| D.科学家利用鱼的沉浮原理制造潜水艇. |
为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )
| A.4,6,1,7 | B.7,6,1,4 | C.6,4,1,7 | D.1,6,4,7 |
下图是选修1-2第二章“推理与证明”的知识结构图,如果要加入“综合法”,则应该放在( )
| A.“合情推理”的下位 | B.“演绎推理”的下位 |
| C.“直接证明”的下位 | D.“间接证明”的下位 |
现有两个推理:①在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”;
②由“若数列 为等差数列,则有
为等差数列,则有 成立”类比 “若数列
成立”类比 “若数列 为等比数列,则有
为等比数列,则有 成立”,则得出的两个结论
成立”,则得出的两个结论
| A.只有①正确 | B.只有②正确 |
| C.都正确 | D.都不正确 |
下面使用类比推理恰当的是 ( )
| A.“若a·3=b·3,则a=b”类推出“若a·0=b·0,则a=b” |
B.“(a+b)c=ac+bc”类推出“ = =  + + ” ” |
C.“(a+b)c=ac+bc”类推出“ = =  + + (c≠0)” (c≠0)” |
| D.“(ab)n=anbn”类推出“(a+b)n = an+bn” |
若大前提是:任何实数的平方都大于0,小前提是: ,结论是:
,结论是: ,那么这个演绎推理出错在:( )
,那么这个演绎推理出错在:( )
| A.大前提出错 | B.小前提出错 | C.推理过程出错 | D.没有出错 |
试题篮
()