利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( )

| A.46 | B.48 | C.50 | D.52 |
如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )
| A.65 | B.64 | C.63 | D.62 |
在样本颇率分布直方图中,共有9个小长方形,若中间一个小长方形的面积等于它8个长方形的面积和的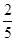 ,且祥本容量为140,则中间一组的频数为( )
,且祥本容量为140,则中间一组的频数为( )
| A.28 | B.40 | C.56 | D.60 |
某班有学生55人,现将所有学生按1,2,3,…,55随机编号.若采用系统抽样的方法抽取一个容量为5的样本,已知编号为 号学生在样本中,则
号学生在样本中,则 _____.
_____.
2013年2月20日,针对房价过高,国务院常务会议确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):
| 月收入(百元) |
赞成人数 |
| [15,25) |
8 |
| [25,35) |
7 |
| [35,45) |
10 |
| [45,55) |
6 |
| [55,65) |
2 |
| [65,75) |
1 |
(I)试根据频率分布直方图估计这60人的平均月收入;
(Ⅱ)若从月收入(单位:百元)在[15,25),[25,35)的被调查者中各随机选取3人进行追踪调查,记选中的6人中不赞成“国五条”的人数为X,求随机变量X的分布列及数学期望.
甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的 次预赛成绩记录如下:甲:
次预赛成绩记录如下:甲: ,
, ,
, ,
, ,
, 乙:
乙: ,
, ,
, ,
, ,
,
(1)用茎叶图表示这两组数据;(2)求甲、乙两人的成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适说明理由?
如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.从这个茎叶图可以看出甲、乙两名运动员得分的中位数分别是( ).

| A.31,26 | B.36,23 | C.36,26 | D.31,23 |
某学校对高二年级一次考试进行抽样分析.右图是根据抽样分析后的考试成绩绘制的频率分布直方图,其中抽样成绩的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[ 104,106].已知样本中成绩小于100分的人数是36,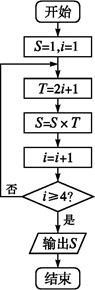 则样本中成绩大于或等于98分且小于104分的人数是( )
则样本中成绩大于或等于98分且小于104分的人数是( )
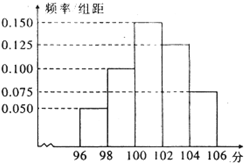
| A.90 | B.75 | C.60 | D.45 |
在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两个样本的下列数字特征相同的是( )
| A.众数 | B.平均数 | C.中位数 | D.标准差 |
学校举办运动会时,高一(1)班有28名同学参加比赛,有15人参加游泳比赛,有8人参加田径比赛,有14人参加球类比赛,同时参加游泳和田径比赛的有3人,同时参加游泳和球类比赛的有3人,没有人同时参加三项比赛.则同时参加田径和球类比赛的人数是( ).
| A.3 | B.4 | C.5 | D.6 |
如图是一容量为 的样本的重量的频率分布直方图,则由图可估计样本的平均重量为( )
的样本的重量的频率分布直方图,则由图可估计样本的平均重量为( )
A. |
B. |
C. |
D. |
某校为了了解高三学生的身体状况,抽取了 名女生,测量其体重.将所得的数据整理后,画出了如图所示的频率分布直方图,则所抽取的女生中体重在
名女生,测量其体重.将所得的数据整理后,画出了如图所示的频率分布直方图,则所抽取的女生中体重在 的人数是
的人数是 
试题篮
()