乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用 局
局 胜制(即先胜
胜制(即先胜 局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同,那么甲以
局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同,那么甲以 比2获胜的概率为( )
比2获胜的概率为( )
A. |
B. |
C. |
D. |
口袋内放有大小相同的2个红球和1个白球,有放回地每次摸取一个球,定义数列{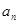 }为
}为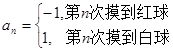 .如果
.如果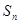 为数列{
为数列{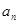 }的前
}的前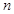 项和,那么
项和,那么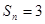 的概率为 ( )
的概率为 ( )
A.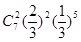 |
B. |
C.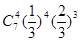 |
D.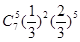 |
甲、乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即以先赢2局者为胜.根据经验,每局比赛中甲获胜的概率为0.6,则本次比赛中甲以2:1的比分获胜的概率为( )
| A.0.288 | B.0.144 | C.0.432 | D.0.648 |
在10个球中有6个红球和4个白球(各不相同),不放回地依次摸出2个球,在第一次摸出红球的条件下,第2次也摸到红球的概率为( )
A.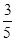 |
B. |
C.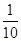 |
D.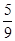 |
假设每一架飞机的引擎在飞行中出现故障的概率为1-p,且各引擎是否有故障是独立的,已知4引擎飞机中至少有3个引擎正常运行,飞机就可成功飞行;2个引擎飞机要2个引擎全部正常运行,飞机才可成功飞行.要使4个引擎飞机更安全,则p的取值范围是
A.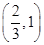 |
B.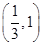 |
C.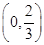 |
D.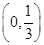 |
试题篮
()