已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.
①求甲射击一次,命中不足8环的概率.
②求甲射击一次,至少命中7环的概率.
甲、乙、丙3人投篮,投进的概率分别是 ,
,  ,
, 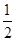 .(Ⅰ)现3人各投篮1次,求3人都没有投进的概率;(Ⅱ)用ξ表示乙投篮3次的进球数,求随机变量ξ的概率分布及数学期望Eξ
.(Ⅰ)现3人各投篮1次,求3人都没有投进的概率;(Ⅱ)用ξ表示乙投篮3次的进球数,求随机变量ξ的概率分布及数学期望Eξ
某种种子每粒发芽的概率都为0.9,现播种了1 000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X,则X的均值为( )
| A.100 | B.200 | C.300 | D.400 |
有甲,乙两个盒子,甲盒中装有2个小球,乙盒中装有3个小球,每次随机选取一个盒子并从中取出一个小球
(1)当甲盒中的球被取完时,求乙盒中恰剩下1个球的概率;
(2)当第一次取完一个盒子中的球时,另一个盒子恰剩下 个球,求
个球,求 的分布列及期望
的分布列及期望 。
。
口袋内装有100个大小相同的红球、白球和黑球,其中有45个红球;从中摸出1个球,若摸出白球的概率为0.23,则摸出黑球的概率为____________.
(本题分12分)
从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同.
(Ⅰ)若抽取后又放回,抽取3次,求恰好抽到2次为红球的概率;
(Ⅱ)若抽取后不放回,设抽完红球所需的次数为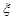 ,求
,求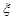 的分布列及期望.
的分布列及期望.
两个人射击,甲射击一次中靶概率是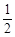 ,乙射击一次中靶概率是
,乙射击一次中靶概率是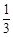 ,
,
(Ⅰ)两人各射击一次,中靶至少一次就算完成目标,则完成目标概率是多少?
(Ⅱ)两人各射击2次,中靶至少3次就算完成目标,则完成目标的概率是多少?
(Ⅲ)两人各射击5次,是否有99%的把握断定他们至少中靶一次?
2010年世博会于5月1日在中国上海隆重开幕,甲、乙、丙三人打算利用周六去游览,由于时间有限,三人商定在已圈定的10个国家馆中各自随机选择一个国家馆游览(选择每个国家馆的可能性相同).
(Ⅰ)求甲、乙、丙三人同时游览同一个国家馆的概率;
(Ⅱ)求甲、乙、丙三人中至少有两人同时游览同一个国家馆的概率.
甲、乙、丙三人在同一办公室工作,办公室只有一部电话机,给该机打进的电话是打给甲、乙、丙的概率分别是 ,在一段时间内该电话机共打进三个电话,且各个电话之间相互独立,则这三个电话中恰有两个是打给乙的概率是 (用分数作答)
,在一段时间内该电话机共打进三个电话,且各个电话之间相互独立,则这三个电话中恰有两个是打给乙的概率是 (用分数作答)
试题篮
()