下面玩掷骰子放球的游戏:若掷出1点,甲盒中放入一球;若掷出2点或是3点,乙盒中放入一球;若掷出4点或5点或6点,丙盒中放入一球.设掷n次后,甲、乙、丙盒内的球数分别为x,y,z.
(1)当n=3时,求x、y、z成等差数列的概率;
(2)当n=6时,求x、y、z成等比数列的概率;
(3)设掷4次后,甲盒和乙盒中球的个数差的绝对值为ξ,求Eξ.
某项考试按科目 、科目
、科目 依次进行,只有当科目
依次进行,只有当科目 成绩合格时,才可继续参加科目
成绩合格时,才可继续参加科目 的考试.
的考试. 已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目
已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目 每次考试成绩合格的概率均为
每次考试成绩合格的概率均为 ,科目
,科目 每次考试成绩合格的概率均为
每次考试成绩合格的概率均为 .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响.
(1)求他不需要补考就可获得证书的概率;
(2)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为 ,
,
求
 的数学期望
的数学期望 .
.
(本小题满分12分)
甲、乙、丙三人按下面的规则进行乒乓球比赛 :第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或
:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或 打满6局时停止.设在每局中参赛者胜负的概率均为
打满6局时停止.设在每局中参赛者胜负的概率均为 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求:
(1)打了两局就停止比赛的概率;
(2)打满3局比赛还未停止的概率;
(3)比赛停止时已打局数 的分布列与期望
的分布列与期望 .
.
一次单元测验由20个选择 题构成,每个选择题有4个选项,其中有且仅有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分.学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选择中随机地选择一个,求学生甲和乙在这次英语单元测验中的成绩的期望
题构成,每个选择题有4个选项,其中有且仅有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分.学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选择中随机地选择一个,求学生甲和乙在这次英语单元测验中的成绩的期望
已知某射手射击一次,击中目标的概率是 .(1)求连续射击5次,恰有3次击中目标的概率;
.(1)求连续射击5次,恰有3次击中目标的概率;
(2)求连续射击5次,击中目标的次数X的数学期望和方差.
(3)假设连续2次未击中目标,则中止其射击,求恰好射击5次后,被中止射击的概率.(本题结果用分数表示即可).
在一次运动会上,某单位派出了有6名主力队员和5名替补队员组成的代表队参加比赛.如果随机抽派5名队员上场比赛,将主力队员参加比赛的人数记为X,求随机变量X的概率分布以及随机变量X数学期望;(本题结果用分数表示即可)
甲、乙两人各射击3次,甲每次击中目标的概率为 ,乙每次击中目标的概率为
,乙每次击中目标的概率为 ,
,
(1)记甲击中目标的次数为 ,求随机变量
,求随机变量 的概率分布表及数学期望
的概率分布表及数学期望 ;
;
(2)求乙至多击中目标2次的概率;
(3)求甲恰好比乙多击中目标2次的概率.
因冰雪灾害,某柑橘基地果林严重收损,为此有关专家提出一种拯救果树的方案,该方案需分两年实施且相互独立。该方案预计第一年可以使柑橘产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.2、0.4、0.4;第二年可以使柑橘产量为第一年的1.5倍、1.25倍、1.0倍的概率分别是0.3、0.3、0.4,求两年后柑橘产量恰好达到灾前产量的概率.
湖南大学自主招生选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为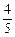 、
、 、
、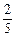 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(1)求该选手被淘汰的概率;
(2)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数学期望
(本小题满分12分)
某同学 参加3门课程的考试.假
参加3门课程的考试.假 设该同学第一门课程取得优秀成绩的概率为
设该同学第一门课程取得优秀成绩的概率为 ,第二、第三门课程取得优秀成绩的概率分别为p,q(p>q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p>q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
| ξ |
0 |
1 |
2 |
3 |
| p |
 |
a |
b |
 |
(I)求该生至少有1门课程取得优秀成绩的概率;
(II)求p,q的值;
(III)求数学期望Eξ.
(本小题满分12分)某项选拔共有三轮考核,每轮设有一问题,能正确回答问题者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、轮的问题的概率分别为 且各轮问题能否正确回答互不影响.
且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选择中回答问题的个数记为 ,求随机变量
,求随机变量 的分布列与数学期望.(注:本小题结果可用分数表示)
的分布列与数学期望.(注:本小题结果可用分数表示)
(本小题满分10分)一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数:f1(x)=x,f2(x)=x2,f3(x)=x3,f4(x)=sinx,f5(x)=cosx,f6(x)=2.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数 的分布列和数学期望.
的分布列和数学期望.
某射手每次射击击中目标的概率是 ,且各次射击的结果互不影响.
,且各次射击的结果互不影响.
(Ⅰ)假设这名射手射击5次,求恰有2次击中目标的概率
(Ⅱ)假设这名射手射击5次,求有3次连续击中目标,另外2次未击中目标的概率
(Ⅲ)假设这名射手射击3次,每次射击,击中目标得1分,未击中目标得0分,在3次射击中,若有2次连续击中,而另外1次未击中,则额外加1分;若3次全击中,则额外加3分,记ξ为射手射击3次后的总得分数,求ξ的分布列
试题篮
()