高中数学随机思想的发展解答题

下面玩掷骰子放球的游戏：若掷出1点，甲盒中放入一球；若掷出2点或是3点，乙盒中放入一球；若掷出4点或5点或6点，丙盒中放入一球．设掷n次后，甲、乙、丙盒内的球数分别为x，y，z.
(1)当n＝3时，求x、y、z成等差数列的概率；
(2)当n＝6时，求x、y、z成等比数列的概率；
(3)设掷4次后，甲盒和乙盒中球的个数差的绝对值为ξ，求Eξ.

学校为绿化环境，移栽了甲、乙两种大树各2株．设甲、乙两种大树移栽的成活率分别为和，且各株大树是否成活互不影响．
（Ⅰ）求移栽的4株大树中恰有3株成活的概率；
（Ⅱ）设移栽的4株大树中成活的株数为,求分布列与期望．

.（本小题满分12分）
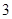若盒中装有同一型号的灯泡共只，其中有只合格品，只次品.
( 1 ) 某工人师傅有放回地连续从该盒中取灯泡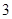次，每次取一只灯泡，求“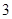次中次取到次品”的概率；
( 2 ) 某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡，每次从中取一灯泡，若是正品则用它更换已坏灯泡，若是次品则将其报废(不再放回原盒中)，求“成功更换会议室的已坏灯泡前取出的次品灯泡只数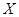”的分布列和数学期望.

盒子里装有大小相同的个球，其中个号球，个号球，个号球.
（1）若第一次从盒子中任取一个球，放回后第二次再任取一个球，求第一次与第二次取到球的号码和是的概率；
（2）若从盒子中一次取出个球，记取到球的号码和为随机变量，求的分布列及期望.

已知函数
（Ⅰ）若，求函数有零点的概率；
（Ⅱ）若是区间上的两个均匀随机数，求函数有零点的概率

甲、乙两名工人加工同一种零件，两人每天加工的零件数相等，所出次品数分别为，，且和的分布列为：

	0	1	2

 
试比较两名工人谁的技术水平更高．

随机抽取某中学甲、乙两班各10名同学，测量他们的身高(单位：cm)，获得身高数据的茎叶图如图所示．

(1)根据茎叶图判断哪个班的平均身高较高；
(2)计算甲班的样本方差；
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学，求身高176cm的同学被抽中的概率．

（本小题满分12分）深圳市于2014年12月29日起实施小汽车限购政策．根据规定，每年发放10万个小汽车名额，其中电动小汽车占20%，通过摇号方式发放，其余名额通过摇号和竞价两种方式各发放一半．政策推出后，某网站针对不同年龄段的申请意向进行了调查，结果如下表所示：

申请意向 年龄	摇号	竞价（人数）	合计
电动小汽车（人数）	非电动小汽车（人数）
30岁以下 （含30岁）	50	100	50	200
30至50岁 （含50岁）	50	150	300	500
50岁以上	100	150	50	300
合计	200	400	400	1000

 
（1）采取分层抽样的方式从30至50岁的人中抽取10人，求其中各种意向人数；
（2）在（1）中选出的10个人中随机抽取4人，求其中恰有2人有竞价申请意向的概率；
（3）用样本估计总体，在全体市民中任意选取4人，其中摇号申请电动小汽车意向的人数记为，求的分布列和数学期望．

某校从参加高三年级第一学期期末考试的学生中抽出50名学生，并统计了他们的数学成绩（成绩均为整数，满分为100分），将数学成绩进行分组并根据各组人数制成如下频率分布表：
（Ⅰ）将上面的频率分布表补充完整，并估计本次考试全校85分以上学生的比例；
（Ⅱ）为了帮助成绩差的同学提高数学成绩，学校决定成立“二帮一”小组，即从成绩为中任选出两位同学，共同帮助成绩在中的某一个同学，试列出所有基本事件；若同学成绩为43分，同学成绩为95分，求、两同学恰好被安排在“二帮一”中同一小组的概率．

分 组	频 数	频 率
[40, 50 ）	2	0.04
[ 50, 60 ）	3	0.06
[ 60, 70 ）	14	0.28
[ 70, 80 ）	15	0.30
[ 80, 90 ）
[ 90, 100 ]	4	0.08
合 计

 

某项新技术进入试用阶段前必须对其中三项不同指标甲、乙、丙进行通过量化检测。假设该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为，指标甲、乙、丙检测合格分别记4分、2分、4分，若某项指标不合格，则该项指标记0分，各项指标检测结果互不影响。
（Ⅰ）求该项技术量化得分不低于8分的概率；
（Ⅱ）记该技术的三个指标中被检测合格的指标个数为随机变量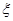，求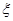的分布列与数学期望。

（本小题满分12分）有4个小盒子，编号为1，2，3，4，将3个小球随机的投入其中（每个盒子容纳小球的个数没有限制），求：
（Ⅰ）第一个盒子为空盒的概率；
（Ⅱ）小球最多的盒子中小球个数的概率分布和期望．

河南省某示范性高中为了推进新课程改革，满足不同层次学生的需求，决定从高一年级开始，在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座，每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座，也可以放弃任何一门科目的辅导讲座（规定：各科达到预先设定的人数时称为满座，否则称为不满座）．统计数据表明，各学科讲座各天的满座概率如下表：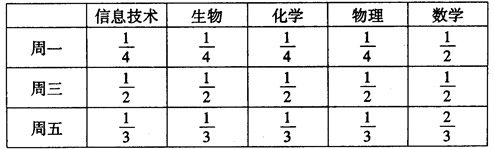

（Ⅰ）求数学辅导讲座在周一、周三、周五都不满座的概率；
（Ⅱ）设周三各辅导讲座满座的科目数为ξ，求随机变量ξ的分布列和数学期望．

某校的学生记者团由理科组和文科组构成，具体数据如下表所示：

组别	理科	文科
性别	男生	女生	男生	女生
人数	4	4	3	1

学校准备从中选出4人到社区举行的大型公益活动进行采访，每选出一名男生，给其所在小组记1分，每选出一名女生则给其所在小组记2分，若要求被选出的4人中理科组、文科组的学生都有．(Ⅰ)求理科组恰好记4分的概率？
(Ⅱ)设文科男生被选出的人数为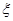，求随机变量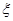的分布列和数学期望．

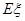（本小题满分12分）某饮料公司招聘了一名员工，现对其进行一项测试，以使确定工资级别，公司准备了两种不同的饮料共8杯，其颜色完全相同，并且其中4杯为A饮料，另外4杯为B饮料，公司要求此员工一一品尝后，从8杯饮料中选出4杯A饮料，若4杯都选对，则月工资定为3500元，若4杯选对3杯，则月工资定为2800元，否则月工资定为2100元，令X表示此人选对A饮料的杯数，假设此人对A和B两种饮料没有鉴别能力．
（1）求X的分布列；
（2）求此员工月工资的期望.

在进行一项掷骰子放球游戏中，规定：若掷出1点，甲盒中放一球；若掷出2点或3点，乙盒中放一球；若掷出4点或5点或6点，丙盒中放一球，前后共掷3次，设分别表示甲，乙，丙3个盒中的球数．
（Ⅰ）求依次成公差大于0的等差数列的概率；
（Ⅱ）求随机变量z的概率分布列和数学期望．