下列命题为特称命题的是( )
| A.偶函数的图像关于y轴对称 | B.正四棱柱都是平行六面体 |
| C.不相交的两条直线是平行直线 | D.存在大于等于3的实数 |
命题“在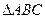 中,若
中,若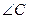 是直角,则
是直角,则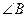 一定是锐角.”的证明过程如下:
一定是锐角.”的证明过程如下:
假设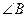 不是锐角,则
不是锐角,则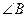 是直角或钝角,即
是直角或钝角,即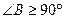 ,
,
所以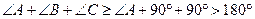 ,
,
这与三角形的内角和等于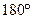 矛盾,所以上述假设不成立,
矛盾,所以上述假设不成立,
所以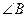 一定是锐角.
一定是锐角.
本题采用的证明方法是
| A.综合法 | B.分析法 | C.反证法 | D.数学归纳法 |
以下四个命题既是特称命题,又是真命题的是( )
| A.斜三角形的内角是锐角或钝角 | B.存在一个负数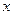 ,使 ,使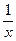 >2 >2 |
| C.两个无理数的和必是无理数 | D.至少有一个实数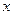 ,使 ,使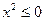 |
命题“三角形中最多只有一个内角是直角”的结论的否定是
| A.有两个内角是直角 | B.有三个内角是直角 |
| C.至少有两个内角是直角 | D.没有一个内角是直角 |
给出下列命题
①若直线 与平面
与平面 内的一条直线平行,则
内的一条直线平行,则 ∥
∥ ;
;
②若平面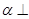 平面
平面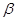 ,且
,且 ,则过
,则过 内一点
内一点 与
与 垂直的直线垂直于平面
垂直的直线垂直于平面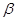 ;
;
③ ;
;
④已知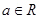 ,则“
,则“ ”是“
”是“ ”的必要不充分条件.
”的必要不充分条件.
其中正确命题的个数是
| A.4 | B.3 | C.2 | D.1 |
已知命题p: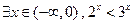 ;命题q:
;命题q: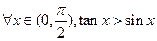 ,则下列命题为真命题的是 ( )
,则下列命题为真命题的是 ( )
| A.p∧q | B.p∨(﹁q) | C.(﹁p)∧q | D.p∧(﹁q) |
试题篮
()