某个命题与正整数n有关,如果当 时命题成立,那么可推得当
时命题成立,那么可推得当 时命题也成立. 现已知当
时命题也成立. 现已知当 时该命题不成立,那么可推得( )
时该命题不成立,那么可推得( )
| A.当n=6时该命题不成立 | B.当n=6时该命题成立 |
| C.当n=8时该命题不成立 | D.当n=8时该命题成立 |
某个命题与正整数有关,若当 时该命题成立,那么可推得当
时该命题成立,那么可推得当
 时该命题也成立,现已知当
时该命题也成立,现已知当 时该命题不成立,那么可推得
时该命题不成立,那么可推得
A.当 时,该命题不成立 时,该命题不成立 |
B.当 时,该命题成立 时,该命题成立 |
C.当 时,该命题成立 时,该命题成立 |
D.当 时,该命题不成立 时,该命题不成立 |
利用数学归纳法证明  时,从“
时,从“ ”变到“
”变到“ ”时,左边应增乘的因式是
”时,左边应增乘的因式是
A. |
B.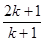 |
C. |
D. |
用数学归纳法证明“(n+1)(n+2)·…·(n+n)=2n·1·3·…·(2n-1)”,从“k到k+1”左端需增乘的代数式为( )
| A.2k+1 | B.2(2k+1) | C. |
D. |
用数学归纳法证明 ,从
,从 到
到 ,左边需增乘的代数式为( )
,左边需增乘的代数式为( )
A. |
B. |
C. |
D. |
某个与自然数有关的命题:如果当n=k( )时,命题成立,则可以推出n=k+1时,该命题也成立.现已知n=6时命题不成立( ).
)时,命题成立,则可以推出n=k+1时,该命题也成立.现已知n=6时命题不成立( ).
| A.当n=5时命题不成立 | B.当n=7时命题不成立 |
| C.当n=5时命题成立 | D.当n=8时命题成立 |
用数学归纳法证明“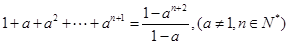 ”时,在验证
”时,在验证 成立时,左边应该是( )
成立时,左边应该是( )
A.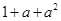 |
B.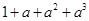 |
C.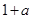 |
D.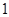 |
用数学归纳法证明 (
( )时,从“
)时,从“ 到
到 ”左边需增乘的代数式为( )
”左边需增乘的代数式为( )
A. |
B. |
C. |
D. |
试题篮
()