(本题12分)已知函数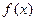 是定义在R上的奇函数,当
是定义在R上的奇函数,当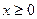 时,
时,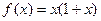 . 求:(
. 求:( 1)
1)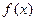 的解析式. (2)画出
的解析式. (2)画出 的图像.
的图像.
某工厂生产一种机器的固定成本为5000元,且每生产100部,需要增加投入2500元,对销售市场进行调查后得知,市场对此产品的需求量为每年500部。已知年销售收入为 ,其中x是产品售出的数量
,其中x是产品售出的数量 。
。
(1 )若x为年产量,y 表示年利润,求
)若x为年产量,y 表示年利润,求 的表达式。(年利
的表达式。(年利 润=年销售收入—投资成本(包括固定成本))
润=年销售收入—投资成本(包括固定成本))
(2)当年产量为何值时,工厂的年利润最大,其最大值是多少?
(本小题满分12分)
某投资公司投资甲乙两个项目所获得的利润分别是M(亿元)和N(亿元),它们与投资额 (亿元)的关系有经验公式:
(亿元)的关系有经验公式: ,今该公司将3亿元投资这个项目,若设甲项目投资
,今该公司将3亿元投资这个项目,若设甲项目投资 亿元,投资这两个项目所获得的总利润为
亿元,投资这两个项目所获得的总利润为 亿元.
亿元.
(I)写出 关于
关于 的函数表达式;
的函数表达式;
(II)求总利润 的最大值.
的最大值.
设二次函数 ,对任意实数
,对任意实数 ,有
,有 恒成立;数列
恒成立;数列 满足
满足 .
.
(1)求函数 的解析式;
的解析式;
(2)试写出一个区间 ,使得当
,使得当 时,
时, 且数列
且数列 是递增数列,并说明理由;
是递增数列,并说明理由;
(3)已知 ,是否存在非零整数
,是否存在非零整数 ,使得对任意
,使得对任意 ,都有
,都有
 恒成立,若存在,求之;若不存在,说明理由.
恒成立,若存在,求之;若不存在,说明理由.
为了降低能源损耗,最近某地对新建住宅的屋顶和外墙都要求建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度 (单位:cm)满足关系:
(单位:cm)满足关系: ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求 的值及
的值及 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用 达到最小,并求最小值.
达到最小,并求最小值.
(本小题满分12分)
已知f(x)是R上的偶函数,且在(0,+  )上单调递增,并且f (x)<0对
)上单调递增,并且f (x)<0对 一切
一切 成立,试判断
成立,试判断 在(-
在(- ,0)上的单调性,并证明你的结论
,0)上的单调性,并证明你的结论
(本小题满分12分)
如图,用长为1的铁丝弯成下部为矩形,上部为半圆形的框架,若半圆半径为x,求此框架围成的面积y与x的函数式y=f (x),并写出它的定义域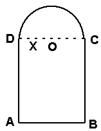
试题篮
()