高中数学三面角、直三面角的基本性质解答题

设函数是定义域为的奇函数．
(Ⅰ)求的值；
(Ⅱ)若，且在上的最小值为，求的值.

已知函数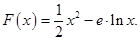
（I）求函数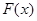的最小值；
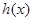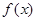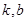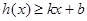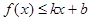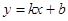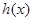（II）对于函数和定义域内的任意实数,若存在常数,使得不等式和都成立,则称直线是函数和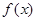的“分界线”．
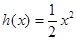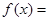
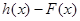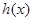设函数，，试问函数和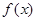是否存在“分界线”？若存在，求出“分界线”的方程．若不存在请说明理由．

已知函数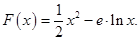
（I）求函数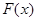的极值；
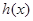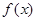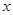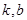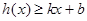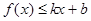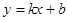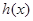（II）对于函数和定义域内的任意实数,若存在常数,使得不等式和都成立,则称直线是函数和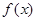的“分界线”．
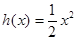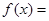
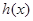设函数，，试问函数和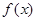是否存在“分界线”？若存在，求出“分界线”的方程．若不存在请说明理由．

已知函数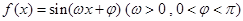在一个周期内的部分对应值如下表：

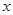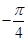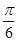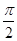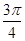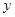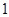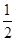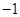（I）求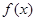的解析式；
（II）设函数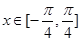，，求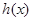的最大值和最小值．

随着机构改革工作的深入进行，各单位要减员增效。有一家公司现有职员人，(，且为偶数)，每人每年可创利万元。据评估，在经营条件不变的前提下，每裁员1人，则留岗职员每人每年可多创利万元，但公司需支付下岗职员每人每年万元的生活费，并且该公司正常运转所需人数不得小于现有员工的,为获得最大的经济效益,该公司应裁员多少人?

已知函数 f（x）=ax＋lnx，其中a为常数，设e为自然对数的底数．
（1）当a=－1时，求的最大值；
（2）若f（x）在区间（0，e］上的最大值为－3，求a的值；
（3）当a=－1时，试推断方程是否有实数解 .

设 
（1）当，求的取值范围；
（2）若对任意，恒成立，求实数的最小值．

某单位设计的两种密封玻璃窗如图所示：图1是单层玻璃，厚度为8 mm；图2是双层中空玻璃，厚度均为4 mm，中间留有厚度为的空气隔层．根据热传导知识，对于厚度为的均匀介质，两侧的温度差为，单位时间内，在单位面积上通过的热量，其中为热传导系数．假定单位时间内，在单位面积上通过每一层玻璃及空气隔层的热量相等．（注：玻璃的热传导系数为，空气的热传导系数为．）

（1）设室内，室外温度均分别为，，内层玻璃外侧温度为，外层玻璃内侧温度为，且．试分别求出单层玻璃和双层中空玻璃单位时间内，在单位面积上通过的热量（结果用，及表示）；
（2）为使双层中空玻璃单位时间内，在单位面积上通过的热量只有单层玻璃的4%，应如何设计的大小？

甲厂以 $x$千克/小时的速度匀速生产某种产品（生产条件要求 $1\le x\le 10$），每一小时可获得的利润是 $100(5x+1-\frac{3}{x})$元．
（1）求证：生产 $a$千克该产品所获得的利润为 $100a\left(5+\frac{1}{x}-\frac{3}{x^2}\right)$元；
（2）要使生产900千克该产品获得的利润最大，问：甲厂应该选取何种生产速度？并求此最大利润．

设不等式 $\left|x-2\right|<a(a\in N^{{*}^{}})$的解集为A,且 $\frac{3}{2}\in A,\frac{1}{2}\notin A$.

（Ⅰ）求 $a$的值

（Ⅱ）求函数 $f\left(x\right)=\left|x+a\right|+\left|x-2\right|$的最小值

已知函数，
（1）若，求的范围；   （2）不等式对任意恒成立，求实数的取值范围。

(1)化简；
(2)已知且，求的值.

已知函数.
（Ⅰ）讨论函数的单调性；
（Ⅱ）设，证明：对任意，.

为了在夏季降温和冬季供暖时减少能源损耗，房屋的房顶和外墙需要建造隔热层，某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元，该建筑物每年的能源消耗费用为C（单位：万元）与隔热层厚度x（单位：cm）满足关系：C（x）=（0x10），若不建隔热层，每年能源消耗费用为8万元。设f（x）为隔热层建造费用与20年的能源消耗费用之和。
(1)求k的值及f(x)的表达式；
(2)隔热层修建多厚时，总费用f（x）达到最小，并求最小值。

已知某公司生产某品牌服装的年固定成本为10万元，每生产千件需另投入2.7万元，设该公司年内共生产该品牌服装千件并全部销售完，每千件的销售收入为万元，且．
(1）写出年利润（万元）关于年产品（千件）的函数解析式；
(2）年产量为多少千件时，该公司在这一品牌服装的生产中所获年利润最大？
(注：年利润=年销售收入－年总成本）