下面给出的四个命题中:
①若m=﹣2,则直线(m+2)x+my+1=0与直线(m﹣2)x+(m+2)y﹣3=0相互垂直;
②命题“∃x∈R,使得x2+3x+4=0”的否定是“∀x∈R,都有x2+3x+4≠0”;
③将函数y=sin2x的图象向右平移 个单位,得到函数
个单位,得到函数 的图象.
的图象.
其中是真命题的有 (将你认为正确的序号都填上).
给出下列四个命题:
(1)命题“若 ,则tanα=1”的逆否命题为假命题;
,则tanα=1”的逆否命题为假命题;
(2)命题p:∀x∈R,sinx≤1.则¬p:∃x0∈R,使sinx0>1;
(3)“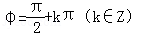 ”是“函数y=sin(2x+ϕ)为偶函数”的充要条件;
”是“函数y=sin(2x+ϕ)为偶函数”的充要条件;
(4)命题p:“∃x0∈R,使 ”;命题q:“若sinα>sinβ,则α>β”,那么(¬p)∧q为真命题.
”;命题q:“若sinα>sinβ,则α>β”,那么(¬p)∧q为真命题.
其中正确的个数是( )
| A.1 | B.2 | C.3 | D.4 |
已知f(x)=3sinx﹣πx,命题p:∀x∈(0, ),f(x)<0,则( )
),f(x)<0,则( )
A.p是假命题,¬p:∀x∈(0, ),f(x)≥0 ),f(x)≥0 |
B.p是假命题,¬p:∃x0∈(0, ),f(x0)≥0 ),f(x0)≥0 |
C.p是真命题,¬p:∀x∈(0, ),f(x)>0 ),f(x)>0 |
D.p是真命题,¬p:∃x0∈(0, ),f(x0)≥0 ),f(x0)≥0 |
下列命题中,正确的是( )
| A.存在x0>0,使得x0<sinx0 |
| B.“lna>lnb”是“10a>10b”的充要条件 |
C.若sinα≠ ,则α≠ ,则α≠ |
| D.若函数f(x)=x3+3ax2+bx+a2在x=﹣1有极值0,则a=2,b=9或a=1,b=3 |
设直线系 :
:
 ,对于下列四个命题:
,对于下列四个命题:
① 中所有直线均经过一个定点;
中所有直线均经过一个定点;
②存在定点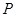 不在
不在 中的任一条直线上;
中的任一条直线上;
③对于任意整数 ,存在正
,存在正 边形,其所有边均在
边形,其所有边均在 中的直线上;
中的直线上;
④ 中的直线所能围成的正三角形面积都相等
中的直线所能围成的正三角形面积都相等
其中真命题的代号是 .(写出所有真命题的代号)
若存在实常数 和
和 ,使得函数
,使得函数 和
和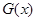 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线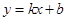 为
为 和
和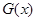 的“隔离直线”,已知函数
的“隔离直线”,已知函数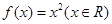 ,
, ,
, ,有下列命题:
,有下列命题:
① 在
在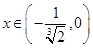 内单调递增;
内单调递增;
② 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且 的最小值为
的最小值为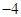 ;
;
③ 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且 的取值范围是
的取值范围是 ;·
;·
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数为 (请填所有正确命题的序号)
给出下列四个命题:
①如果命题“¬p”与命题“p∨q”都是真命题,那么命题q一定是真命题;
②命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”;
③若命题p:∃x≥0,x2﹣x+1<0,则¬p:∀x<0,x2﹣x+1≥0;
④设{an}是首项大于零的等比数列,则“a1<a2”是“数列{an}是递增数列”的充分而不必要条件.
其中为真命题的个数是( )
| A.4个 | B.3个 | C.2个 | D.1个 |
下列命题中为真命题的是( )
| A.命题“若x>1,则x2>1”的否命题 |
| B.命题“若x>y,则|x|>y”的逆命题 |
C.若k<5,则两椭圆 与 与 有不同的焦点 有不同的焦点 |
| D.命题“若方程x2+ky2=2表示焦点在y轴上的椭圆,则k的取值范围为(0,1)”的逆否命题 |
有四个命题
①p:f(x)=lnx﹣2+λ在区间(1,2)上有一个零点,q:e0.2>e0.3,p∧q为真命题
②当x>1时,f(x)=x2,g(x)=x ,h(x)=x﹣2的大小关系是h(x)<g(x)<f(x)
,h(x)=x﹣2的大小关系是h(x)<g(x)<f(x)
③若f′(x0)=0,则f(x)在x=x0处取得极值
④若不等式2﹣3x﹣2x2>0的解集为P,函数y= +
+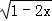 的定义域为Q,则“x∈P”是“x∈Q”的充分不必要条件,其中正确命题的个数是( )
的定义域为Q,则“x∈P”是“x∈Q”的充分不必要条件,其中正确命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
给出如下四个命题:
①若“p且q”为假命题,则p、q均为假命题;
②命题“若a>b,则2a>2b﹣1”的否命题为“若a≤b,则2a≤2b﹣1”;
③“∀x∈R,x2+1≥1”的否定是“∃x∈R,x2+1≤1;
④在△ABC中,“A>B”是“sinA>sinB”的充要条件.
其中不正确的命题的个数是( )
| A.4 | B.3 | C.2 | D.1 |
试题篮
()