已知函数 ,在定义域
,在定义域 上表示的曲线过原点,且在
上表示的曲线过原点,且在 处的切线斜率均为
处的切线斜率均为 .有以下命题:
.有以下命题:
① 是奇函数;②若
是奇函数;②若 在
在 内递减,则
内递减,则 的最大值为4;③
的最大值为4;③ 的最大值为
的最大值为 ,最小值为
,最小值为 ,则
,则 ; ④若对
; ④若对 ,
, 恒成立,则
恒成立,则 的最大值为2.其中正确命题的序号为
的最大值为2.其中正确命题的序号为
若存在实常数 和
和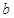 ,使得函数
,使得函数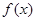 和
和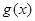 对其定义域上的任意实数
对其定义域上的任意实数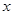 分别满足:
分别满足: 和
和 ,则称直线
,则称直线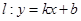 为
为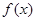 和
和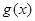 的“隔离直线”.已知函数
的“隔离直线”.已知函数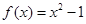 和函数
和函数 ,那么函数
,那么函数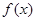 和函数
和函数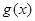 的隔离直线方程为_________.
的隔离直线方程为_________.
已知函数f(x)=xlnx,过点A  作函数y=f(x)图象的切线,则切线的方程为________.
作函数y=f(x)图象的切线,则切线的方程为________.
已知P(-1,1),Q(2,4)是曲线f(x)=x2上的两点,则平行于直线PQ的曲线
y=x2的切线方程是________________.
若曲线y=x2+ax+b在点(0,b)处的切线方程为x-y+1=0,则a,b的值分别为________,________.
设函数f(x)= D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为 .
D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为 .
若曲线f(x)=ax2+lnx存在垂直于y轴的切线,则实数a的取值范围是 .
若曲线y=x- 在点(m,m-
在点(m,m- )处的切线与两坐标轴围成三角形的面积为18,则m=________.
)处的切线与两坐标轴围成三角形的面积为18,则m=________.
试题篮
()