已知命题 :函数
:函数 为
为 上单调减函数,实数
上单调减函数,实数 满足不等式
满足不等式 .命题
.命题 :当
:当 ,函数
,函数 .若命题
.若命题 是命题
是命题 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围。
的取值范围。
已知圆C的极坐标方程为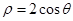 ,直线l的参数方程为
,直线l的参数方程为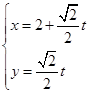 (t为常数,t∈R)
(t为常数,t∈R)
(Ⅰ)求直线l的普通方程和圆C的直角坐标方程;
(Ⅱ)求直线l与圆C相交的弦长.
如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合,已知AE的长为m,AC的长为n,AD,AB关于x的方程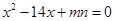 的两个根.
的两个根.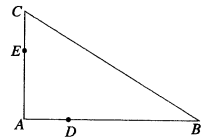
(Ⅰ)证明:C、B、D、E四点共圆;
(Ⅱ)若∠A=90°,且m=4,n=6,求C、B、D、E所在圆的半径.
已知函数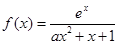 ,其中a∈R,
,其中a∈R,
(Ⅰ)若a=0,求函数f(x)的定义域和极值;
(Ⅱ)当a=1时,试确定函数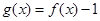 的零点个数,并证明.
的零点个数,并证明.
已知在直角坐标系xOy中,直线l的参数方程为 ,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设点P是曲线C上的一个动点,求它到直线l的距离d的取值范围.
已知AB为半圆O的直径,AB=4,C为半圆上一点,过点C作半圆的切线CD,过点A作AD⊥CD于D,交半圆于点E,DE=1.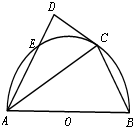
(Ⅰ)求证:AC平分∠BAD;
(Ⅱ)求BC的长.
如图,在直三棱柱 中,平面
中,平面
 侧面
侧面 且
且 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若直线AC与平面 所成的角为
所成的角为 ,求锐二面角
,求锐二面角 的大小.
的大小.
现有4个人去参加娱乐活动,该活动有甲、乙两个游戏可供参加者选择,为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏。
(Ⅰ)求这4个人中恰有2人去参加甲游戏的概率;
(Ⅱ)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(Ⅲ)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记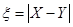 ,求随机变量
,求随机变量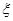 的分布列与数学期望
的分布列与数学期望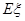 .
.
在△A BC,a,b,c分别是角A,B,C的对边,且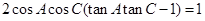 .
.
(Ⅰ)求B的大小;
(Ⅱ)若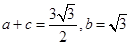 ,求△A BC的面积.
,求△A BC的面积.
试题篮
()