已知椭圆 的左焦点为
的左焦点为 ,离心率为
,离心率为 ,点M在椭圆上且位于第一象限,直线
,点M在椭圆上且位于第一象限,直线 被圆
被圆 截得的线段的长为c,
截得的线段的长为c, .
.
(Ⅰ)求直线 的斜率;
的斜率;
(Ⅱ)求椭圆的方程;
(Ⅲ)设动点 在椭圆上,若直线
在椭圆上,若直线 的斜率大于
的斜率大于 ,求直线
,求直线 (
( 为原点)的斜率的取值范围.
为原点)的斜率的取值范围.
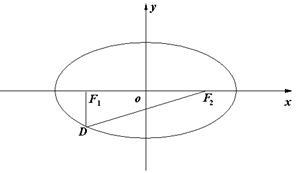
如图,设椭圆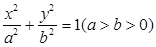 的左.右焦点分别为
的左.右焦点分别为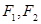 ,点
,点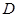 在椭圆上,
在椭圆上,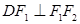 ,
,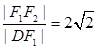 ,
,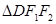 的面积为
的面积为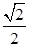 .
.
(1)求该椭圆的标准方程;
(2)设圆心在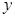 轴上的圆与椭圆在
轴上的圆与椭圆在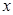 轴的上方有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径.
轴的上方有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径.
设 ,
, 分别是椭圆
分别是椭圆 的左右焦点,M是C上一点且
的左右焦点,M是C上一点且 与x轴垂直,直线
与x轴垂直,直线 与C的另一个交点为N.
与C的另一个交点为N.
(1)若直线MN的斜率为 ,求C的离心率;
,求C的离心率;
(2)若直线MN在y轴上的截距为2,且 ,求a,b.
,求a,b.
已知椭圆 的下顶点为
的下顶点为 ,
, 到焦点的距离为
到焦点的距离为 .
.
(Ⅰ)设Q是椭圆上的动点,求 的最大值;
的最大值;
(Ⅱ)若直线 与圆O:
与圆O: 相切,并与椭圆
相切,并与椭圆 交于不同的两点A、B.当
交于不同的两点A、B.当 ,且满足
,且满足 时,求
时,求 AOB面积S的取值范围.
AOB面积S的取值范围.
已知抛物线 的顶点为原点,其焦点
的顶点为原点,其焦点 到直线
到直线 :
: 的距离为
的距离为 .设
.设 为直线
为直线 上的点,过点
上的点,过点 作抛物线
作抛物线 的两条切线
的两条切线 ,其中
,其中 为切点.
为切点.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)当点 为直线
为直线 上的定点时,求直线
上的定点时,求直线 的方程;
的方程;
(Ⅲ)当点 在直线
在直线 上移动时,求
上移动时,求 的最小值.
的最小值.
无穷数列 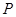 :
: ,
,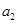 ,……,
,……,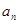 ,……,满足
,……,满足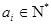 ,且
,且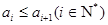 ,对于数列
,对于数列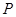 ,记
,记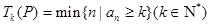 ,其中
,其中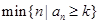 表示集合
表示集合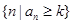 中最小的数.
中最小的数.
(1)若数列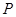 :1,3,4,7,……,写出
:1,3,4,7,……,写出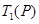 ,
,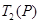 ,……,
,……,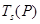 ;
;
(2)若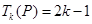 ,求数列
,求数列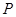 前
前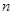 项的和;
项的和;
(3)已知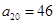 ,求
,求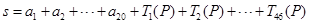 的值.
的值.
试题篮
()