(本小题满分12分)
按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活动(以下简称活动).某校高一·一班50名学生在上学期参加活动的次数统计如条形图所示.
(Ⅰ)求该班学生参加活动的人均次数 ;
;
(Ⅱ)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率;
(Ⅲ)从该班中任选两名学生,用 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .(要求:答案用最简分数表示)
.(要求:答案用最简分数表示)
选修4-1:几何证明选讲
△ABC内接于⊙O,AB=AC,直线MN切⊙O于C,弦BD∥MN,AC、BD交于点E
(1)求证:△ABE≌△ACD
(2)AB=6,BC=4,求AE
已知圆 为圆上一动点,点
为圆上一动点,点 在
在 上,点
上,点 在
在 上,且满足
上,且满足 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)若直线 与(1)中所求点
与(1)中所求点 的轨迹
的轨迹 交于不同两点
交于不同两点 是坐
是坐
标原点,且 ,求△
,求△ 的面积的取值范围.
的面积的取值范围.
如图所示,四棱锥P—ABCD中,AB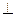 AD,CD
AD,CD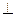 AD,PA
AD,PA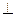 底面ABCD,PA=AD=CD=2AB=2,M为PC的中点。
底面ABCD,PA=AD=CD=2AB=2,M为PC的中点。
(1)求证:BM∥平面PAD;
(2)在侧面PAD内找一点N,使MN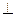 平面PBD;
平面PBD;
(3)求直线PC与平面PBD所成角的正弦。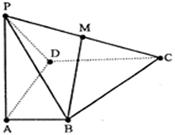
已知数列{an}满足a1=1,a2=3,an+2=3an+1-2an(n∈N+)
(1)证明:数列{an+1-an }是等比数列;
(2)求数列{an}的通项公式
(本小题满分14分)
如图所示,椭圆C: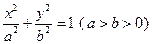 的两个焦点为
的两个焦点为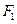 、
、 ,短轴两个端点为
,短轴两个端点为 、
、 .已知
.已知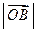 、
、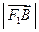 、
、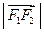 成等比数列,
成等比数列, ,与
,与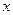 轴不垂直的直线
轴不垂直的直线 与C 交于不同的两点
与C 交于不同的两点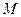 、
、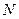 ,记直线
,记直线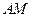 、
、 的斜率分别为
的斜率分别为 、
、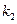 ,且
,且 .
.
(Ⅰ)求椭圆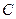 的方程;
的方程;
(Ⅱ)求证直线 与
与 轴相交于定点,并求出定点坐标;
轴相交于定点,并求出定点坐标;
(Ⅲ)当弦 的中点
的中点 落在四边形
落在四边形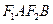 内(包括边界)时,求直线
内(包括边界)时,求直线 的斜率的取值范围.
的斜率的取值范围.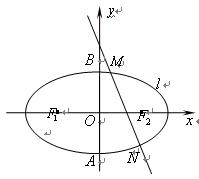
(本小题满分12分)
函数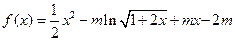 ,其中
,其中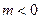 .
.
(Ⅰ)试讨论函数 的单调性;
的单调性;
(Ⅱ)已知当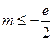 (其中
(其中 是自然对数的底数)时,在
是自然对数的底数)时,在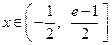 上至少
上至少
存在一点 ,使
,使 成立,求
成立,求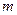 的取值范围;
的取值范围;
(Ⅲ)求证:当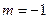 时,对任意
时,对任意 ,
,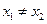 ,有
,有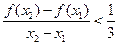 .
.
(本小题满分12分)
已知 是各项都为正数的数列,其前
是各项都为正数的数列,其前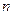 项和为
项和为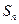 ,且满足
,且满足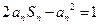 .
.
(Ⅰ)求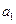 ,
,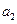 ,
, 的值;
的值;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)令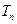 =
=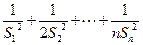 ,求证
,求证 .
.
(本小题满分12分)
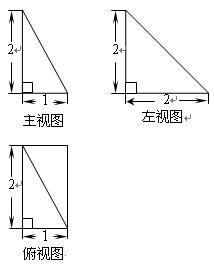
已知四棱锥 的直观图和三视图如图所示,
的直观图和三视图如图所示,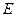 是
是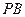 的中点.
的中点.
(Ⅰ)若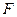 是
是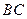 上任一点,求证:
上任一点,求证: ;
;
(Ⅱ)设 ,
,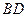 交于点
交于点 ,求直线
,求直线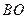 与平面
与平面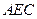 所成角的正弦值.
所成角的正弦值.
试题篮
()