高中数学解答题

在平面直角坐标系xOy中，设点集 $A_n=\left\{\right(0,0),(1,0),(2,0),\dots ,(n,0\left)\right\}$ ， $B_n=\left\{\right(0,1),(n,1)\text{}},C_n=\{(0,2),(1,2),(2,2),\cdots ,(n,2)\},n\in N^{*}.$   

令 $M_n=A_n\cup B_n\cup C_n$ .从集合 M _n中任取两个不同的点，用随机变量 X表示它们之间的距离.

（1）当 n=1时，求 X的概率分布；    

（2）对给定的正整数 n（ n≥3），求概率 P（ X≤ n）（用 n表示）.

设 ${(1+x)}^n=a_0+a_{1}x+a_2{x}^2+\cdots +a_n{x}^n,n⩾4,n\in N^{*}$ .已知 $a_3^2=2a_2{a}_4$ .   

（1）求 n的值；    

（2）设 ${(1+\sqrt{3})}^n=a+b\sqrt{3}$ ，其中 $a,b\in N^{*}$ ，求 $a^2-3b^2$ 的值.    

设 $x\in R$ ，解不等式 $\text{|}x\text{|+|2}x-\text{1|>2}$ .   

在极坐标系中，已知两点 $A(3,\frac{\pi }{4}),B(\sqrt{2},\frac{\pi }{2})$ ，直线l的方程为 $\rho \sin (\theta +\frac{\pi }{4})=3$ .

（1）求 A， B两点间的距离；    

（2）求点 B到直线 l的距离.    

已知矩阵 $A=\left[\begin{array}{cc}3& 1\\ 2& 2\end{array}\right]$

（1）求 A ²；    

（2）求矩阵 A的特征值.   

定义首项为1且公比为正数的等比数列为"M－数列".   

（1）已知等比数列{ a _n} $(n\in N^{*})$ 满足： $a_2{a}_4=a_5,a_3-4a_2+4a_4=0$ ，求证:数列{ a _n}为"M－数列"；    

（2）已知数列{ b _n}满足: $b_1=1,\frac{1}{S_n}=\frac{2}{b_n}-\frac{2}{b_{n+1}}$ ，其中 S _n为数列{ b _n}的前 n项和．

①求数列{ b _n}的通项公式；

②设 m为正整数，若存在"M－数列"{ c _n} $(n\in N^{*})$ ，对任意正整数 k ，当 k≤ m时，都有 $c_k⩽b_k⩽c_{k+1}$ 成立，求 m的最大值．

设函数 $f\left(x\right)=(x-a)(x-b)(x-c),a,b,c\in \text{R}$ 、 $f\text{'}\left(x\right)$ 为f（x）的导函数．   

（1）若 a= b= c ， f（4）=8，求 a的值；    

（2）若 a≠ b ， b= c ， 且 f（ x）和 $f\text{'}\left(x\right)$ 的零点均在集合 $\text{{}-3,1,3\text{}}$ 中，求 f（ x）的极小值；    

（3）若 $a=0,0<b⩽1,c=1$ ，且 f（ x）的极大值为 M，求证: M≤ $\frac{4}{27}$ ．

如图，一个湖的边界是圆心为O的圆，湖的一侧有一条直线型公路l ，湖上有桥AB（AB是圆O的直径）．规划在公路l上选两个点P、Q ，并修建两段直线型道路PB、QA ．规划要求:线段PB、QA上的所有点到点O的距离均不小于圆O的半径．已知点A、B到直线l的距离分别为AC和BD（C、D为垂足），测得AB=10，AC=6，BD=12（单位:百米）．

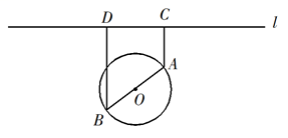
（1）若道路PB与桥AB垂直，求道路PB的长；   

（2）在规划要求下，P和Q中能否有一个点选在D处？并说明理由；   

（3）对规划要求下，若道路PB和QA的长度均为d（单位：百米）.求当d最小时，P、Q两点间的距离．

如图，在平面直角坐标系xOy中，椭圆C: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的焦点为F ₁（-1、0），F ₂（1，0）．过F ₂作x轴的垂线l ，在x轴的上方，l与圆F ₂: ${(x-1)}^2+y^2=4a^2$ 交于点A ，与椭圆C交于点D.连结AF ₁并延长交圆F ₂于点B ，连结BF ₂交椭圆C于点E ，连结DF ₁．已知DF ₁= $\frac{5}{2}$ ．

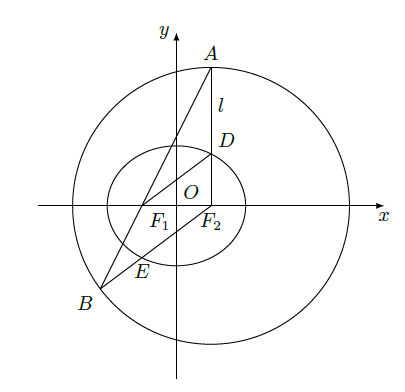
（1）求椭圆 C的标准方程；    

（2）求点 E的坐标．    

如图，在直三棱柱ABC－A ₁B ₁C ₁中，D ， E分别为BC ， AC的中点，AB=BC ．  

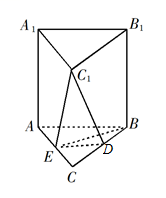
求证：

（1） A ₁ B ₁∥平面 DEC ₁；    

（2） BE⊥ C ₁ E．    

在△ABC中，角A ， B ， C的对边分别为a ， b ， c

（1）若 a=3 c ， b= $\sqrt{2}$ ，cos B= $\frac{2}{3}$ ，求 c的值；

（2）若 $\frac{\sin A}{a}=\frac{\cos B}{2b}$ ，求 $\sin (B+\frac{\pi }{2})$ 的值．

设定义在R上的函数f（x）满足：对于任意的x ₁、x ₂∈R，当x ₁＜x ₂时，都有f（x ₁）≤f（x ₂）.

（1）若f（x）=ax ³+1，求a的取值范围；

（2）若f（x）是周期函数，证明：f（x）是常值函数；

（3）设f（x）恒大于零，g（x）是定义在R上的、恒大于零的周期函数，M是g（x）的最大值．函数h（x）=f（x）g（x）．证明："h（x）是周期函数"的充要条件是"f（x）是常值函数"．

在平面直角坐标系xOy中，已知椭圆Γ： $\frac{x^2}{4}+y^2$ =1，A为Γ的上顶点，P为Γ上异于上、下顶点的动点，M为x正半轴上的动点．

（1）若P在第一象限，且|OP|= $\sqrt{2}$ ，求P的坐标；

（2）设P（ $\frac{8}{5}，\frac{3}{5}$ ），若以A、P、M为顶点的三角形是直角三角形，求M的横坐标；

（3）若|MA|=|MP|，直线AQ与Γ交于另一点C，且 $\overrightarrow{\mathit{AQ}}=2\overrightarrow{\mathit{AC}}$ ， $\overrightarrow{\mathit{PQ}}=4\overrightarrow{\mathit{PM}}$ ，求直线AQ的方程．

根据预测，某地第n（n∈N ^*）个月共享单车的投放量和损失量分别为a _n和b _n（单位：辆），其中a _n= $\{\begin{array}{c}5n^4+15{，}_{}1\le n\le 3\\ -10n+470{，}_{}n\ge 4\end{array}$ ，b _n=n+5，第n个月底的共享单车的保有量是前n个月的累计投放量与累计损失量的差．    

（1）求该地区第4个月底的共享单车的保有量；    

（2）已知该地共享单车停放点第n个月底的单车容纳量S _n=﹣4（n﹣46） ²+8800（单位：辆）．设在某月底，共享单车保有量达到最大，问该保有量是否超出了此时停放点的单车容纳量？

已知函数f（x）=cos ²x﹣sin ²x+ $\frac{1}{2}$ ，x∈（0，π）．    

（1）求f（x）的单调递增区间；    

（2）设△ABC为锐角三角形，角A所对边a= $\sqrt{19}$ ，角B所对边b=5，若f（A）=0，求△ABC的面积．