高中数学解答题

（本小题满分14分）
已知点到直线l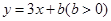：的距离为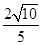.数列{a_n}的首项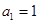，且点列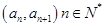均在直线l上.
（Ⅰ)求b的值；
（Ⅱ）求数列{a_n}的通项公式；
（Ⅲ）求数列的前n项和.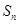

（本小题满分14分）如图所示，某海岛上一观察哨A在上午11时测得一轮船在海岛北偏东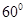的C处，12时20分测得船在海岛北偏西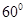的B处，12时40分轮船到达位于海岛正西方且距海岛5km的E港口，如果轮船始终匀速直线前进，问船速多少？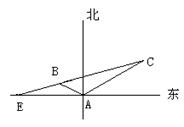

（本小题满分14分）等比数列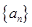的各项均为正数，且
（Ⅰ)求数列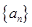的通项公式；
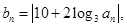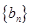（Ⅱ）设求数列的前n项和；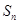
（III）设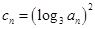,求证：

（本小题满分12分）已知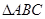三个顶点的直角坐标分别为A(3，4)、B(0，0)、C(c，0)．
（Ⅰ)若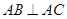,求c的值；       
（Ⅱ）若c=5，求sin∠A的值．

（本小题满分12分）
（Ⅰ）求以下不等式的解集：
（1）       （2）
（Ⅱ）若关于x的不等式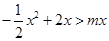的解集为，求实数m的值．

（本小题满分12分）已知f（x）=ax²（a∈R）, g（x）="2lnx."
（1）讨论函数F（x）=f（x）-g（x）的单调性；
（2）是否存在实数a，使得f（x）≥g（x）+2 （x>0）恒成立，若不存在，请说明理由；若存在，求出a的取值范围;
（3）若方程f（x）=g（x）在区间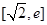上有两个不相等的实数根，求a的取值范围.

（本小题10分）若函数，当时，函数有极值．
（1）求函数的解析式；
（2）若方程有3个不同的实根，求实数的取值范围．

（本小题8分）机器按照模具生产的产品也会有缺陷，我们将有缺陷的产品称为次品，每小时出现的次品数随机器运转速度的不同而变化．下表为某机器生产过程的数据：

速度x（百转/秒）	2	4	5	6	8
每小时生产次品数y（个）	30	40	50	60	70

 
（1）求机器运转速度与每小时生产的次品数之间的回归方程；
（2）若实际生产所允许的每小时生产的次品数不超过75件，那么机器的速度（百转/秒）不超过多少？（写出满足题目的整数解）

．（本小题8分）已知二次函数在处取得极值，且在点处的切线与直线平行． 
（1）求函数的单调递增区间；
（2）求函数在的最值.

（本小题8分）全国人民代表大会在北京召开，为了搞好对外宣传工作，会务组选聘了16名男记者和14名女记者担任对外翻译工作．调查发现，男、女记者中分别有10人和6人会俄语．
（1）根据以上数据完成以下列联表：

	会俄语	不会俄语	总计
男
女
总计

 
（2）能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关？

（本小题满分12分）已知f（x）=ax²（a∈R）, g（x）=2lnx．
（1）讨论函数F（x）=f（x）-g（x）的单调性；
（2）是否存在实数a，使得f（x）≥g（x）+2 （x>0）恒成立，若不存在，请说明理由；若存在，求出a的取值范围；
（3）若方程f（x）=g（x）在区间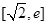上有两个不相等的实数根，求a的取值范围．

（本小题8分）已知数列的前项和．
（1）计算，，，；
（2）猜想的表达式，并用数学归纳法证明你的结论．

（本小题满分8分） 已知函数．
（1）求函数f（x）的单调区间；
（2）已知a、b∈R,a>b>e, （其中e是自然对数的底数）, 求证:b^a >a^b．

（本小题满分8分） 已知抛物线C：y=-x²+4x-3 ．
（1）求抛物线C在点A（0，－3）和点B（3，0）处的切线的交点坐标；
（2）求抛物线C与它在点A和点B处的切线所围成的图形的面积．

（本小题满分14分）在的展开式中，把叫做三项式系数．
（Ⅰ）当时，写出三项式系数的值；
（Ⅱ）二项式的展开式中，系数可用杨辉三角形数阵表示，如图：

当时，类似杨辉三角形数阵表，请列出三项式的次系数列的数阵表；
（Ⅲ）求的值（可用组合数作答）．