在直角坐标系 中,曲线 的方程为 .以坐标原点为极点, 轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为 .
(1)求 的直角坐标方程;
(2)若 与 有且仅有三个公共点,求 的方程.
设抛物线 ,点 , ,过点 的直线 与 交于 , 两点.
(1)当 与 轴垂直时,求直线 的方程;
(2)证明: .
某家庭记录了未使用节水龙头 天的日用水量数据(单位: )和使用了节水龙头 天的日用水量数据,得到频数分布表如下:
未使用节水龙头 天的日用水量频数分布表
| 日用水量 |
|
|
|
|
|
|
|
| 频数 |
|
|
|
|
|
|
|
使用了节水龙头 天的日用水量频数分布表
| 日用水量 |
|
|
|
|
|
|
| 频数 |
|
|
|
|
|
|
(1)在答题卡上作出使用了节水龙头 天的日用水量数据的频率分布直方图:
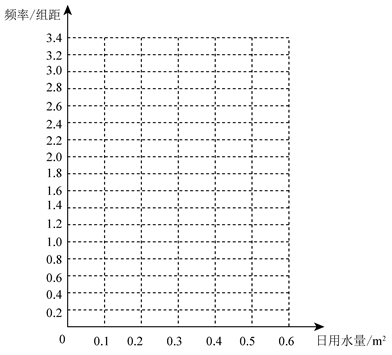
(2)估计该家庭使用节水龙头后,日用水量小于 的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按 天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
如图,在平行四边形
中,
,
,以
为折痕将△
折起,使点
到达点
的位置,且  .
.
(1)证明:平面 平面 ;
(2)
为线段
上一点,
为线段
上一点,且 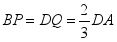 ,求三棱锥
,求三棱锥 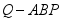 的体积.
的体积.

已知数列 满足 , ,设 .
(1)求 ;
(2)判断数列 是否为等比数列,并说明理由;
(3)求 的通项公式.
在直角坐标系 中,曲线 的参数方程为 ( 为参数),直线 的参数方程为 ( 为参数).
(1)求 和 的直角坐标方程;
(2)若曲线 截直线 所得线段的中点坐标为 ,求 的斜率.
设抛物线 的焦点为 ,过 且斜率为 的直线 与 交于 , 两点, .
(1)求 的方程;
(2)求过点 , 且与 的准线相切的圆的方程.
如图,在三棱锥 中, , , 为 的中点.
(1)证明: 平面 ;
(2)若点 在棱 上,且 ,求点 到平面 的距离.
下图是某地区2000年至2016年环境基础设施投资额 (单位:亿元)的折线图.

为了预测该地区2018年的环境基础设施投资额,建立了 与时间变量 的两个线性回归模型.根据2000年至2016年的数据(时间变量 的值依次为 )建立模型①: ;根据2010年至2016年的数据(时间变量 的值依次为 )建立模型②: .
(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.
试题篮
()