如图所示,为光电计时器的实验简易示意图,当有不透光物体从光电门间通过时,光电计时器就可以显示物体的挡光时间,实验中所选用的光电门传感器可测的最短时间为0.01ms.光滑水平导轨MN上放两个相同物块A和B,其宽度a =3.0×10-2m,左端挡板处有一弹射装置P,右端N处与水平传送带平滑连接,今将挡光效果好,宽度为d =3.6×10-3m的两块黑色磁带分别贴在物块A和B上,且高出物块,并使高出物块部分在通过光电门时挡光.传送带水平部分的长度L =8m,沿逆时针方向以恒定速度v =6m/s匀速传动.物块A、B与传送带间的动摩擦因数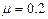 ,质量mA =mB =1kg.开始时在A和B之间压缩一轻弹簧,锁定其处于静止状态,现解除锁定,弹开物块A和B,迅速移去轻弹簧,两物块第一次通过光电门,计时器显示读数均为t =9.0×10-4s. g取10m/s2.试求:
,质量mA =mB =1kg.开始时在A和B之间压缩一轻弹簧,锁定其处于静止状态,现解除锁定,弹开物块A和B,迅速移去轻弹簧,两物块第一次通过光电门,计时器显示读数均为t =9.0×10-4s. g取10m/s2.试求:
(1)弹簧储存的弹性势能EP;
(2)物块B沿传送带向右滑动的最远距离sm;
(3)物块B滑回水平面MN的速度大小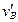 ;
;
(4)若物体B返回水平面MN后与被弹射装置P弹回的物块A在水平面上相碰,且A和B碰后互换速度,则弹射装置P至少必须对物块A做多少功,才能在AB碰后使B刚好能从Q端滑出?此过程中,滑块B与传送带之间因摩擦产生的内能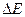 为多大?
为多大?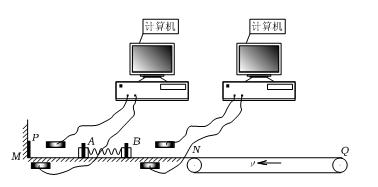
如图所示,一质量m1=0.2kg的小球,从光滑水平轨道上的一端A处,以v1=2.5m/s的速度水平向右运动. 轨道的另一端B处固定放置一竖直光滑半圆环轨道(圆环半径比细管的内径大得多),轨道的半径R=10cm,圆环轨道的最低点与水平轨道相切;空中有一固定长为15cm 的木板DF,F端在轨道最高点C的正下方,竖直距离为5cm。水平轨道的另一端B处有一质量m
的木板DF,F端在轨道最高点C的正下方,竖直距离为5cm。水平轨道的另一端B处有一质量m 2=0.2kg的小球,m1、m2两小球在B处发生的是完全弹性碰撞,重力加速度为g=10m/s2. 求:
2=0.2kg的小球,m1、m2两小球在B处发生的是完全弹性碰撞,重力加速度为g=10m/s2. 求: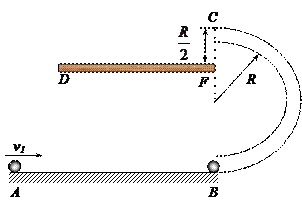
(1)经过C点时,小球m2对轨道的作用力的大小及方向?
(2)m2小球打到木板DF上的位置?
如图所示,AB为一轻质杠杆,O为支点,BO=2AO,AB两端分别悬挂实心铜球和实心铁球,杠杆在水平位置平衡,若将两球同时浸没在某液体中,液体的密度小于铜和铁的密度,则
| A.杠杆仍能保持平衡 | B.铜球一端下降 |
| C.铁球一端下降 | D.液体密度未知,故无法判断哪端下降 |
关于力的合成与分解,下列说法哪个是正确的:
| A.合力的作用效果与分力共同作用的效果相同 |
| B.合力一定比任一个分力大 |
| C.合力的大小一定等于各分力的大小之和 |
| D.求一个已知力的分力,只能按效果分解成一对分力 |
A、B两物体质量分别为m和2m,A置于光滑水平面上,B置于粗糙水平面上,用相同水平力F分别推A和B,使它们前进相同的位移,下面说法正确的是( )
A.两次推力做功相等 B.第二次推力做功大一些
C.第一次推力做功大 D.无法比较
作用于O点的三力平衡,设其中一个力的大小为F1,沿y轴正方向,力F2大小未知,与x轴负方向夹角为θ,如图所示,下列关于第三个力F3的判 断正确的是
断正确的是
| A.力F3只能在第四象限 |
| B.力F3与F2夹角越小,则F2和F3的合力越小 |
| C.F3的最小值为F1cosθ |
| D.力F3可能在第一象限的任意区域 |
两个力F1和F2间的夹角为 ,两力的合力为F。以下说法正确的是
,两力的合力为F。以下说法正确的是
| A.合力F总比分力F1和F2中的任何一个力都大 |
B. 若夹角 若夹角 不变,F1大小不变,只要F2增大,合力F一定增大 不变,F1大小不变,只要F2增大,合力F一定增大 |
C.若夹角 不变,F1和F2同时增大,合力F一定增大 不变,F1和F2同时增大,合力F一定增大 |
D.若F1和F2的大小不变, 角越小,合力越大 角越小,合力越大 |
用如图所示的装置,探究功与物体速度变化的关系。实验时先适当垫高木板,然后由静止释放小车,小车在橡皮筋弹力的作用下被弹出,沿木板滑行。小车滑行过程中带动通过打点计时器的纸带,记录其运动情况。观察发现纸带前面部分点迹疏密不均,后面部分点迹比较均匀,回答下列问题: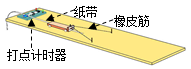
1.适当垫高木板是为了
2.通过纸带求小车速度时,应使用纸带的 (填“全部”、“前面部分”或“后面均匀部分”)
假定轮船在行驶时受到的阻力跟船速成正比,欲使轮船的速度比原来提高一倍,则轮船在单位时间内消耗的燃料为原来的多少倍( )
| A.2 | B.4 | C.8 | D.以上答案都不对 |
如图所示,在水平地面放一质量m=1.0kg的木块,木块与地面间的动摩擦因数μ=0.6,在水平方向上对木块同时施加相互垂直的两个拉力F1、F2.已知F1=3.0N,F2=4.0N.(可认为最大静摩擦力等于滑动摩擦力)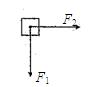
(1)则木块受到的摩擦力为多大?
(2)若将F2顺时针旋转90°,此时木块在水平方向上受到的合力大小为多大?
| 材 料 |
木一金属 |
木一木 |
木一冰 |
钢一钢 |
| 动摩擦因数 |
0.20 |
0.30 |
0.03 |
0.25 |
两个共点力,大小分别是30N 和50N,则两力的合力大小可能是
| A.10N | B.30N | C.50N | D.150N |
如图(1)所示,斜拉桥的塔柱两侧有许多钢索,它们的一端都系在塔柱上.对于每组对称钢索,它们的上端可以看成系在一起,即两根钢索对塔柱的拉力F1、F2作用在同一点.它们合起来对塔柱的作用效果应该让塔柱好像受到一个竖直向下的力F一样,如图(2)所示.这样,塔柱便能稳固地伫立在桥墩上,不会因钢索的牵拉而发生倾斜,甚至倒下.如果斜拉桥塔柱两侧的钢索不能呈对称分布如图(3)所示,要保持塔柱所受的合力竖直向下,那么钢索AC、AB的拉力FAC、FAB应满足
A. B.
B.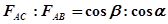
C. D.
D.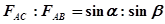
下列各图中,所有接触面都是光滑的,所有物体都处于静止状态.P、Q两个物体之间不存在弹力的是 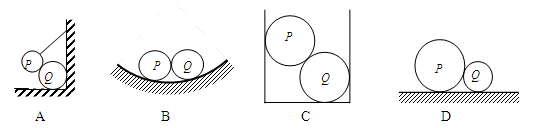
试题篮
()