高中物理相互作用、力与机械试题

如图所示，已知带电小球A、B的电荷量分别为Q_A、Q_B，OA=OB，都用长L的绝缘丝线悬挂在绝缘墙角O点处。静止时A、B相距为d。为使平衡时AB间距离变为2d，可采用以下哪些方法

A．将小球B的质量变为原来的八分之一  
B．将小球B的质量增加到原来的8倍
C．将小球A、B的电荷量都增为原来的二倍，同时将小球B的质量变为原来的一半
D．将小球A、B的电荷量都减小到原来的一半，同时将小球B的质量增加到原来的2倍

如图所示，倾角为的斜面体固定在水平地面上，一根不可伸长的轻绳两端分别系着小球A和物块B，跨过固定于斜面体顶端的定滑轮O（不计滑轮的摩擦），A的质量为m，B的质量为4m．开始时，用手托住A，使OA段绳恰好处于水平伸直状态（绳中无拉力），OB绳平行于斜面，此时B静止不动，将A由静止释放，在其下摆过程中B始终保持静止．则在绳子到达竖直位置之前，下列说法正确的是

A．小球A运动到最低点时物块B所受的摩擦力为mg

B．物块B受到的摩擦力方向没有发生变化

C．若适当增加OA段绳子的长度，物块可能发生运动

D．地面对斜面体的摩擦力方向一定水平向右

如图所示，固定的半球面右侧是光滑的，左侧是粗糙的，O点为球心，A、B为两个完全相同的小物块（可视为质点），小物块A静止在球面的左侧，受到的摩擦力大小为F₁，对球面的压力大小为N₁；小物块B在水平力F₂作用下静止在球面的右侧，对球面的压力大小为N₂，已知两小物块与球心连线和竖直方向的夹角均为θ，则

A．F₁：F₂=cosθ：1                       B．F₁：F₂＝sinθ：1   
C．N₁：N₂＝cos²θ：1                     D.N₁：N₂＝sin²θ：1

如图所示，在光滑的水平面上静止着一个质量为m₂小球2，质量为m₁的小球1以一定的初速度v₁朝着球2运动，如果两球之间、球与墙之间发生的碰撞均无机械能损失，要使两球还能再碰，则两小球的质量需满足怎样的关系？

如图所示，a，b，c三根绳子完全相同，b绳水平，c绳下挂一重物。若增加重物的重量，则最先断的绳子是（  ）

A．a绳

B．b绳

C．c绳

D．无法确定

如图所示，总质量为460kg的热气球，从地面刚开始竖直上升时的加速度为0.5m/s²，当热气球上升到180m时，以5m/s的速度向上匀速运动.若离开地面后热气球所受浮力保持不变，上升过程中热气球总质量不变，所受空气阻力与速度成正比，重力加速度g=10m/s² .关于热气球，下列说法正确的是（ ）

A．所受浮力大小为4830N

B．加速上升过程中热气球处于完全失重状态

C．从地面开始上升10s后的速度大小为5m/s

D．以5m/s匀速上升时所受空气阻力大小为200N

在如下所示的A、B、C、D四图中，滑轮本身的重力忽略不计，滑轮的轴O安装在一根轻木杆P上，一根轻绳ab绕过滑轮，a端固定在墙上，b端下面挂一个质量都是m的重物，当滑轮和重物都静止不动时，A、C、D图中杆P与竖直方向夹角均为θ，图B中杆P在竖直方向上，假设A、B、C、D四图中滑轮受到木杆弹力的大小依次为F_A、F_B、F_C、F_D，则以下判断中正确的是

A．F_A=F_B= F_C=F_D                   B．F_D＞F_A=F_B＞F_C
C．F_A= F_C=F_D＞F_B                           D．F_C＞F_A=F_B＞F_D

(10分)如图所示，质量为m_A=2kg的木块A静止在光滑水平面上。一质量为m_B= 1kg的木块B以某一初速度v₀=5m/s沿水平方向向右运动，与A碰撞后都向右运动。木块A 与挡板碰撞后立即反弹（设木块A与挡板碰撞过程无机械能损失）。后来木块A与B发生二次碰撞，碰后A、B同向运动，速度大小分别为0.9m/s、1.2m/s。求：

①第一次木块A、B碰撞过程中A对B的冲量大小、方向
②木块A、B第二次碰撞过程中系统损失的机械能是多少。

如图所示，作用于坐标原点O的三个力平衡，已知三个力均位于xOy平面内，其中力F₁的大小不变，方向沿y轴负方向；力F₂的大小未知，方向与x轴正方向的夹角为θ．则下列关于力F₃的判断正确的是：

A．力F3只能在第二象限．

B．力F3与F2夹角越小，则F2与F3的合力越小．

C．力F3的最小值为F1cosθ．

D．力F3可能在第三象限的任意区域．

如图(a)所示，轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为M₁的物体，∠ACB＝30°；如图(b)中轻杆HG一端用铰链固定在竖直墙上，另一端G通过细绳EG拉住，EG与水平方向也成30°，轻杆的G点用细绳CF拉住一个质量为M₂的物体，求：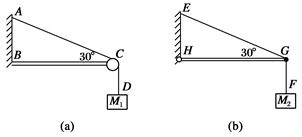

(1)细绳AC段的张力T_AC与细绳EG的张力T_EG之比；
(2)轻杆BC对C端的支持力；
(3)轻杆HG对G端的支持力．

有些人，像电梯修理员、牵引专家和赛艇运动员，常需要知道绳或金属线中的张力，可又不能到那些绳、线的自由端去测量．一家英国公司现在制造出一种夹在绳上的仪表，用一个杠杆使绳子的某点有一个微小偏移量，如图所示，仪表很容易测出垂直于绳的恢复力．推导一个能计算绳中张力的公式．如果偏移量为12 mm，恢复力为300 N，计算绳中张力．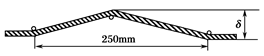

如图为曲柄压榨机结构示意图，A处作用一水平力F，OB是竖直线．若杆和活塞重力不计，两杆AO与AB的长度相同；当OB的尺寸为200，A到OB的距离为10时，求货物M在此时所受压力为多少？

如图所示，能承受最大拉力为10 N的细线OA与竖直方向成45°角，能承受最大拉力为5 N的细线OB水平，细线OC能承受足够的拉力，为使OA、OB均不被拉断，OC下端所悬挂物体的最大重力是多少？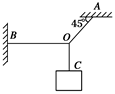

如图所示，这是斧头劈柴的剖面图，图中BC边为斧头背，AB、AC边为斧头的刃面．要使斧头容易劈开木柴，则应该(　　)

A．BC边短一些，AB边也短一 些
B．BC边长一些，AB边短一些
C．BC边短一些，AB边长一些
D．BC边长一些，AB边也长一些

F₁、F₂合力方向竖直向下，若保持F₁的大小和方向都不变，保持F₂的大小不变，而将F₂的方向在竖直平面内转过60°角，合力的方向仍竖直向下，下列说法正确的是(　　)

A．F1一定大于F2

B．F1可能小于F2

C．F2的方向与水平面成30°角

D．F1方向与F2的方向成60°角