高中物理相互作用、力与机械试题

如图所示，固定在水平地面上的物体A，左侧是圆弧面，右侧是倾角为的斜面，一根轻绳两端分别系有质量为、的小球，当两球静止时，小球与圆心连线跟水平方向的夹角也为，不计一切摩擦，则、之间的关系是

A．

B．

C．

D．

一条船由两岸纤夫拉着沿水平面的笔直水渠前进，水流作用可以忽略。岸这边纤夫以恒力拉船，方向如图所示，那么，对岸纤夫朝什么方向拉船时，用力最小？最小值为多少？

用两根轻质的绳子AB和BC吊一个的灯，如果BC绳处于水平，AB绳与水平夹角为，求三绳中的拉力的大小（）。

如图所示，将一球形物体夹在竖直墙AC与木板BC之间，已知各接触面均光滑，将球对墙的压力用表示，球对木板的压力用表示，现将木板以C端为轴缓慢地转至水平位置的过程中，下列说法中正确的是（    ）

A．和都增大	B．和都减小
C．增大，减小	D．减小，增大

已知力的大小为，此力不可以分解成如下（   ）

A．

B．

C．

D．

如图所示，光滑水平地面上有一直角三角形斜面体B靠在竖直墙壁上，物块A放在斜面体B上，开始A、B静止。现用水平力F推A，A、B仍静止，则此时B受力的个数可能是（ ）

A．3个   B．4个      C．5个   D．6个

如图所示，斜面顶端固定有半径为R的轻质滑轮，用不可伸长的轻质细绳将半径为r的球沿斜面缓慢拉升。不计各处摩擦，且R>r。设绳对球的拉力为F，斜面对球的支持力为N，则关于F和N的变化情况，下列说法正确的是（ ）

A．F一直增大，N一直减小

B．F一直增大，N先减小后增大

C．F一直减小，N保持不变

D．F一直减小，N一直增大

位于坐标原点O的质点在F₁、F₂和F₃三力作用下保持静止，已知其中F₁的大小恒定不变，方向沿y轴负方向；F₂的方向与x轴正方向的夹角为θ（θ<45°），但大小未知，如图所示。则下列关于力F₃的判断正确的是（ ）

A．F3的最小值为F1cosθ

B．F3的大小可能为F1sinθ

C．F3的方向可能与F2的方向相反

D．F3与F2的合力大小与F2的大小有关

如图所示，AO、BO、CO是完全相同的绳子，并将钢梁水平吊起，若钢梁足够重时，绳子AO先断，则（ ）

A．θ=120°

B．θ＞120°

C．θ＜120°

D．不论θ为何值，AO总是先断

一根细绳能承受的最大拉力是G，现把一重为 G的物体系在绳的中点，分别握住绳的两端，先并拢，然后缓慢地左右对称地分开，若要求绳不断，则两绳间的夹角不能超过（  ）

A．45°

B．60°

C．120°

D．135°

两个共点力大小都是60N，要使这两个力的合力是30N，这两个力的夹角θ应满足下列哪一项（   ）

A．θ=60°

B．θ=45°

C．θ=30°

D．cos(θ/2)=0.25

如图，物体P静止于固定的斜面上，P的上表面水平，现把物体Q轻轻地叠放在P上，则（   ）

A．P向下滑动	B．P静止不动
C．P所受的合外力增大	D．P与斜面间的静摩擦力增大

如图所示，质量为 M 的三角形木块 a 放在水平面上，把另一质量为 m 的木块 b 放在a 的斜面上，斜面倾角为 α ，对 a 施一水平力 F，使 b 不沿斜面滑动，不计一切摩擦，则b 对 a 的压力大小为 (      )

A．mgcosα	B．Mg/cos α
C．	D．

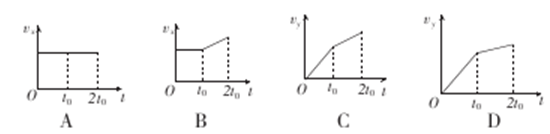
滑雪者从山上M处以水平速度飞出，经t_o时间落在山坡上N处时速度方向刚好沿斜坡向下，接着从N沿直线自由滑下，又经t₀时间到达坡底 P处。斜坡NP与水平面夹角为30°，不计摩擦阻力和空气阻力，则从M到P过程中水平、竖直两方向的分速度ν_x、ν_y随时间变化的图象是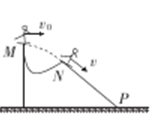

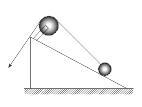
如图所示，将一个表面光滑的铁球放在两块斜面板AB和CD之间，两板与水平面的夹角都是60°。已知重力加速度大小为g，不计空气阻力，则

A．如果突然撤去CD板，则撤去后铁球对AB板的压力减小

B．如果突然撤去CD板，则撤去后铁球对AB板的压力增大

C．如果保持AB板不动，使CD板与水平面的夹角缓慢减小，则球对AB板的压力先减小后增大

D．如果保持AB板不动，使CD板与水平面的夹角缓慢减小，则球对CD板的压力先减小后增大