如图，用OA、OB两根轻绳将花盆悬于两竖直墙之间，开始时OB绳水平．现保持O点位置不变，改变OB绳长使绳右端由B点缓慢上移至B′点，此时OB′与OA之间的夹角θ＜90°．设此过程OA、OB绳的拉力分别为FOA、FOB，则下列说法正确的是（ ）
A．FOA一直减小 B．FOA一直增大
C．FOB一直减小 D．FOB先减小后增大
不在同一直线上的两个共点力
和
的大小不同，夹角为
，它们的合力大小为F，则
| A．合力F可能沿和夹角的角平分线 |
| B．保持和的大小不变，夹角增大，则合力F一定减小 |
| C．保持夹角不变，若和中的一个减小，合力F一定减小 |
| D．保持夹角不变，若和同时增大一倍，合力F也增大一倍 |
如图所示，光滑水平地面上有一直角三角形斜面体B靠在竖直墙壁上，物块A放在斜面体B上，开始A、B静止。现用水平力F推A，A、B仍静止，则此时B受力的个数可能是（ ）
A．3个 B．4个 C．5个 D．6个
如图所示，斜面顶端固定有半径为R的轻质滑轮，用不可伸长的轻质细绳将半径为r的球沿斜面缓慢拉升。不计各处摩擦，且R>r。设绳对球的拉力为F，斜面对球的支持力为N，则关于F和N的变化情况，下列说法正确的是（ ）
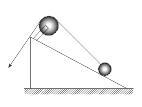
| A．F一直增大，N一直减小 |
| B．F一直增大，N先减小后增大 |
| C．F一直减小，N保持不变 |
| D．F一直减小，N一直增大 |
两个共点力大小都是60N，要使这两个力的合力是30N，这两个力的夹角θ应满足下列哪一项（ ）
| A．θ=60° | B．θ=45° | C．θ=30° | D．cos(θ/2)=0.25 |
如图所示，质量为 M 的三角形木块 a 放在水平面上，把另一质量为 m 的木块 b 放在a 的斜面上，斜面倾角为 α ，对 a 施一水平力 F，使 b 不沿斜面滑动，不计一切摩擦，则b 对 a 的压力大小为 ( )
| A．mgcosα | B．Mg/cos α |
C． |
D． |
如图所示，将一个表面光滑的铁球放在两块斜面板AB和CD之间，两板与水平面的夹角都是60°。已知重力加速度大小为g，不计空气阻力，则
| A．如果突然撤去CD板，则撤去后铁球对AB板的压力减小 |
| B．如果突然撤去CD板，则撤去后铁球对AB板的压力增大 |
| C．如果保持AB板不动，使CD板与水平面的夹角缓慢减小，则球对AB板的压力先减小后增大 |
| D．如果保持AB板不动，使CD板与水平面的夹角缓慢减小，则球对CD板的压力先减小后增大 |
如图甲所示，在圆柱体上放一物块P，圆柱体绕水平轴O缓慢转动，从A转至A′的过程，物块与圆柱体保持相对静止，则图乙反映的是该过程中( )
| A．重力随时间变化的规律 | B．支持力随时间变化的规律 |
| C．摩擦力随时间变化的规律 | D．合外力随时间变化的规律 |
如图所示，一光滑半圆形碗固定在水平面上，质量为m1的小球用轻绳跨过碗口并连接质量分别为m2和m3的物体，平衡时碗内小球恰好与碗之间没有弹力，两绳与水平方向夹角分别为53°、37°，则m1：m2：m3的比值为（已知sin53°=0.8，cos53°=0.6）（ ）
| A．5：4：3 | B．4：3：5 | C．3：4：5 | D．5：3：4 |
已知两个共点力的合力为F，如果它们之间的夹角固定不变，使其中的一个力增大，则
| A．合力F一定增大 | B．合力F的大小可能不变 |
| C．合力F可能增大 | D．合力F可能减小 |
如图所示，小车内有一固定光滑斜面，一个小球通过细绳与车顶相连，小车在水平面上做直线运动，细绳始终保持竖直，关于小球的受力情况，下列说法中正确的是（ ）
| A．若小车静止，绳对小球的拉力可能为零 |
| B．若小车静止，斜面对小球的支持力一定为零 |
| C．若小车向右运动，小球一定受两个力的作用 |
| D．若小车向右运动，小球一定受三个力的作用 |
下列说法正确的是（ ）
| A．两个共点力的合力为一定值，则一个力的两个分力也是定值 |
| B．物体做曲线运动时，其合力的瞬时功率可能为零 |
| C．一对平衡力所做功可能为零，也可能大小相等、一正一负 |
| D．在月球上举重比在地球上容易，所以同一个物体在月球上比在地球上惯性小 |
E．在国际单位制中，质量、长度、时间、电流都属于基本物理量
1800年前，当众人面对大象这样的庞然大物，因为缺少有效的称量工具而束手无策的时候，曹冲想出了称量大象体重的方法，被世人所称道，下列物理学习或研究中用到的方法与“曹冲称象”的方法相同的是（ ）
| A．“质点”的概念 |
| B．合力与分力的关系 |
| C．“瞬时速度”的概念 |
| D．研究加速度与合力、质量的关系 |
试题篮
()
粤公网安备 44130202000953号
