高中物理力矩的平衡条件试题

如图（1）所示，均匀长方体木块长b=18cm，高h=16cm，宽L=10cm，被两个力传感器支撑起来，两传感器间距为a=10cm且到木块两边的距离相等，传感器能够将支撑点的受力情况通过数据采集器在计算机屏幕上反映出来。现用一弹簧测力计水平拉木块，拉力作用在木块的中点且缓慢均匀增大，木块则始终保持静止状态，计算机屏上出现如图（2）所示的图线。问：
图（2）上的直线A反映的是_______________传感器上的受力情况（“左边”或“右边”）弹簧测力计的最大拉力是_______________N。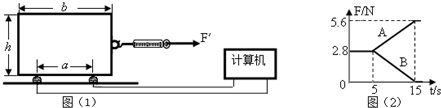

如图所示，轻杆BC的C点用光滑铰链与墙壁固定，杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角．若在B点悬挂一个定滑轮(不计重力)，某人用它匀速地提起重物．已知重物的质量m＝30 kg，人的质量M＝50  kg，g取10 m/s².试求：
(1)此时地面对人的支持力的大小；
(2)轻杆BC和绳AB所受力的大小．

如图所示，两根重杆OA和AB，由铰链连接，并用铰链悬挂在天花板上，B位于O的正下方，若在B端分别施加图示方向的力F₁、F₂、F₃和F₄，则其中可能使两杆保持静止的是（     ）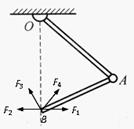

A．F1

B．F2

C．F3

D．F4

直杆AB和直角弯杆BCD按如图所示连接，A、B、D处均为铰链，杆及铰链的质量都不计。ABCD构成一长方形，将重力为G、可视为质点的物块放在图中P处。则

A．AB杆对BCD杆的作用力方向沿BC连线向下
B．BCD杆对AB杆的作用力方向沿DB连线斜向上
C．若AP间距变大，BCD杆对AB杆的作用力变大
D．若AP间距变大，AB杆对BCD杆的作用力对转动轴D的力矩不变

一轻杆BO，其O端用光滑铰链铰于固定竖直杆AO上，B端挂一重物，且系一细绳，细绳跨过杆顶A处的光滑小滑轮，用力F拉住，如图所示．现将细绳缓慢往左拉，使杆 BO与杆AO间的夹角θ逐渐减小，则在此过程中，拉力F及杆BO所受压力F_N的大小变化情况是              (　　)

A．FN先减小，后增大

B．FN始终不变

C．F先减小，后增大

D．F逐渐减小

如图所示，重为Ｇ的圆盘与一轻杆相连，杆与圆盘恰相切，支点为Ｏ。现用始终竖直向下的力F拉杆的另一端，使该端缓慢向下转动，则杆转到竖直之前，拉力F及其力矩Ｍ的变化情况是（     ）

A．Ｍ变小，F不变.	B．Ｍ、F均变小.
C．Ｍ先变大再变小，F始终变大.	D．Ｍ、F均先变大再变小

如图，框架ABC由三根长度均为l、质量均为m的均匀细棒组成，A端用光滑铰链铰接在墙壁上．现用竖直方向的力F作用在C端，使AB边处于竖直方向且保持平衡，则力F的大小为　   　．若在C点施加的作用力改为大小为1.5mg、方向始终垂直于AC边的力F′，使框架从图示位置开始逆时针转动，运动过程中当框架具有最大动能时，力F′所做的功为　   　．

一块木板可绕过O点的光滑水平轴在竖直平面内转动，木板上放有一木块，木板右端受到始终与木板垂直的力F，从图中位置A缓慢转到位置B，木块相对木板不发生滑动。则在此过程中，力F和F的力矩M_F大小的变化情况是（   ）

A．F始终保持不变，MF先变小后变大

B．F始终保持不变，MF先变大后变小

C．F先变大后变小，MF先变小后变大

D．F先变大后变小，MF先变大后变小

如图所示，质量为m、边长为l的等边三角形ABC导线框，在A处用轻质细线竖直悬挂于质量也为m、长度为L的水平均匀硬杆一端，硬杆另一端通过轻质弹簧连接地面，离杆左端L/3处有一光滑固定转轴O。垂直于ABC平面有一个水平方向的匀强磁场，磁感应强度大小为B，当在导线框中通以逆时针方向大小为I的电流时，AB边受到的安培力大小为________，此时弹簧对硬杆的拉力大小为________。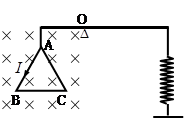

一根粗细均匀的金属棒AB，棒的A端用轻绳同定在天花板上，棒的B端用水平拉力F拉着而使金属棒处于静止状态。轻绳与竖直方向的夹角为α，金属棒与竖直方向的夹角为β，下列说法正确的是

A．sinβ＝2sinα	B．cosβ＝2cosα
C．tanβ＝2tanα	D．cotβ＝2cotα

如图，竖直轻质悬线上端固定，下端与均质硬直棒OB的三分之一处A点连接，悬线长度也为OB的三分之一，棒的O端用水平轴铰接在墙上，棒处于水平状态。改变悬线长度，使线与棒的连接点由A向B逐渐右移，并保持棒始终处于水平状态。则悬线拉力（     ）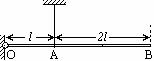

A．逐渐减小	B．逐渐增大
C．先减小后增大	D．先增大后减小

如图为悬挂街灯的支架示意图，横梁BE质量为6kg，重心在其中点。直角杆A.DC重力不计，两端用铰链连接。已知BE=3m，BC=2m，∠A.CB=30°，横梁E处悬挂灯的质量为2kg，则直角杆对横梁的力矩为_______N·m，直角杆对横梁的作用力大小为_______N。（重力加速度g=l0m/s²）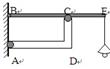

如图所示，一根木棒AB在O点被悬挂起来，AO＝OC，在A、C两点分别挂有两个和三个钩码，木棒处于平衡状态。如在木棒的A、C点各增加一个同样的钩码，则木棒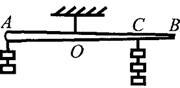

A．绕O点顺时针方向转动

B．绕O点逆时针方向转动

C．平衡可能被破坏，转动方向不定

D．仍能保持平衡状态

水平导轨AB固定在支架CD上，其形状、尺寸如图所示。导轨与支架的总质量M=4kg，其重心在O点，它只能绕支架C点且垂直于纸面的水平轴转动。质量m=1kg的小铁块静止于水平导轨AB的A端，现受到水平拉力F=2.5N的作用。已知小铁块和导轨之间的动摩擦因数μ＝0.2。g取10m/s²，求：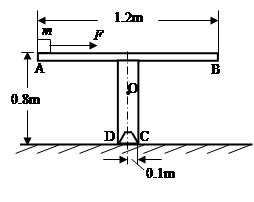

（1）小铁块刚开始运动时的加速度大小？
（2）小铁块运动到离A端多远时，支架将要开始翻转？
（3）若在小铁块运动的过程中，支架始终保持静止，则拉力F作用的最长时间为多少？

塔式起重机的结构如图所示，设机架重P＝400 kN，悬臂长度为L＝10 m，平衡块重W＝200 kN，平衡块与中心线OO^/的距离可在1 m到6 m间变化，轨道A、B间的距离为4 m。

⑴当平衡块离中心线1 m，右侧轨道对轮子的作用力f_B是左侧轨道对轮子作用力f_A的2倍，问机架重心离中心线的距离是多少？
⑵当起重机挂钩在离中心线OO^/10 m处吊起重为G＝100 kN的重物时，平衡块离OO^/的距离为6 m，问此时轨道B对轮子的作用力F_B时多少？