某人把质量为0.1kg的一块小石头从距地面为5m的高处以60°角斜向上抛出,抛出时的初速度大小为10m/s,则当石头着地时,其速度大小约为 ( ) (g取10m/s2)
| A.14m/s | B.12m/s | C.28m/s | D.20m/s |
下列说法正确的是
| A.由能量守恒定律可知,能量不能无中生有 |
| B.风能、水能是太阳能的间接形式 |
| C.人类通过不断努力,永动机是可以制造出来的 |
| D.能量耗散反映了自然界能量转化的方向性 |
起重机竖直吊起质量为m的重物,上升的加速度是α,上升的高度是h,则起重机对货物所做的功是。( )
| A.mgh | B.mαh | C.m(g+α)h | D.m(g-α)h |
如图所示,小球从A点以初速度vo沿粗糙斜面向上运动,到达最高点B后返回A,C为AB的中点。下列说法中正确的是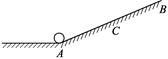
| A.小球从A出发到返回A的过程中,位移为零,外力做功为零 |
| B.小球从A到C与从C到B的过程,减少的动能相等 |
| C.小球从A到C与从C到B的过程,速度的变化率相等 |
| D.小球从A到C与从C到B的过程,损失的机械能相等 |
如图,两个互相垂直的力F1与F2作用在同一物体上,使物体通过一段位移过程中,力F1对物体做功4 J,力F2对物体做功3 J,则力F1与F2的合力对物体做功为: 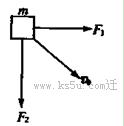
| A.7 J | B.1 J | C.5 J | D.3.5 J |
以初速度v0竖直向上抛出一个质量为m的小球,小球运动过程中所受阻力f的大小不变,上升的最大高度为h,则抛出过程中,人手对小球做的功为(设急速抛出):( )
A.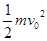 |
B.mgh | C.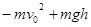 |
D.mgh+fh |
质量为1kg的物体从某一高度自由下落,则该物体下落1 s末重力做功的瞬时功率是(取g = 10m/s2):
| A.25W | B.50W | C.75W | D.100W |
两名质量相等的滑冰人甲和乙都静止在光滑的水平冰面上.现在,其中一人向另一个人抛出一个篮球,另一人接球后再抛回.如此反复进行几次后,甲和乙最后的速率关系是( )
| A.若甲最先抛球,则一定是v甲>v乙 |
| B.若乙最后接球,则一定是v甲>v乙 |
| C.只有甲先抛球,乙最后接球,才有v甲>v乙[来源:Z§xx§k.Com] |
| D.无论怎样抛球和接球,都是v甲>v乙 |
井深10m,井上支架高2m,在支架上用一根4m长的绳子系住一个重100N的物体,则物体的重力势能为(以地面为零重力势能平面):
| A.100J | B.-100J | C.200J | D.-200J |
在“探究弹性势能的表达式”的活动中,为计算弹簧弹力所做的功,把拉伸弹簧的过程分为很多小段,拉力在每小段可以认为是恒力,用各小段做功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”.下面几个实例中应用到这一思想方法的是( )
A.由加速度的定义 ,当 ,当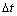 非常小, 非常小,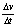 就可以表示物体在t时刻的瞬时加速度 就可以表示物体在t时刻的瞬时加速度 |
| B.在探究加速度、力和质量三者之间关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系 |
| C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加 |
| D.在不需要考虑物体本身的大小和形状时,用有质量的点来代替物体,即质点 |
两个物体质量比为1∶4,速度大小之比为4∶1,则这两个物体的动能之比为( )
| A.1∶1 | B.1∶4 | C.4∶1 | D.2∶1 |
将一小球竖直上抛,若该球所受的空气阻力大小不变,则其上升和下降两过程的时间及损失的机械能的关系是
A. > > , ,  > >  |
B. < < , ,  < <  |
C. < < , ,  = =  |
D. = = , ,  = =  |
从地面竖直上抛两个质量不同而动能相同的物体(不计空气阻力),当上升到同一高度时,它们( )
| A.所具有的重力势能相等 | B.所具有的动能相等 |
| C.所具有的机械能相等 | D.所具有的机械能不等 |
在地面上某处将一金属小球竖直向上抛出,上升一定高度后再落回原处。若不考虑空气阻力,则下列图象能正确反映小球的速度v、加速度a、位移x和动能Ek随时间变化关系的是(取向上为正方向)( )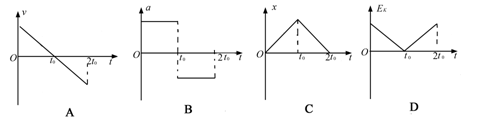
试题篮
()