起重机竖直吊起质量为m的重物,上升的加速度是α,上升的高度是h,则起重机对货物所做的功是。( )
| A.mgh | B.mαh | C.m(g+α)h | D.m(g-α)h |
如图,两个互相垂直的力F1与F2作用在同一物体上,使物体通过一段位移过程中,力F1对物体做功4 J,力F2对物体做功3 J,则力F1与F2的合力对物体做功为: 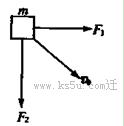
| A.7 J | B.1 J | C.5 J | D.3.5 J |
假定轮船在行驶时受到的阻力跟船速成正比,欲使轮船的速度比原来提高一倍,则轮船在单位时间内消耗的燃料为原来的多少倍( )
| A.2 | B.4 | C.8 | D.以上答案都不对 |
质量为1kg的物体从某一高度自由下落,则该物体下落1 s末重力做功的瞬时功率是(取g = 10m/s2):
| A.25W | B.50W | C.75W | D.100W |
关于机械能守恒定律的适用条件,下列说法中正确的是:
| A.只要有重力和弹力作用时,机械能一定守恒 |
| B.当有其他外力作用时,只要合外力为零,机械能一定守恒 |
| C.当有其他外力作用时,只有重力做功,机械能一定守恒 |
| D.物体只受重力作用的运动,机械能一定守恒 |
关于重力势能,下列说法中正确的是:
| A.某个物体处于某个位置,重力势能的大小是惟一确定的 |
| B.重力势能为零的物体,不可能对别的物体做功 |
| C.物体做匀速直线运动时,其重力势能一定不变 |
| D.只要重力做功,物体的重力势能一定变化 |
质量为m的小球被系在轻绳的一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受到空气阻力的作用。设某一时刻小球通过轨道的最低点,此时绳子的拉力为7mg,此后小球继续做圆周运动,经过半个圆周恰能通过最高点,则在此过程中小球克服空气阻力所做的功为:( )
A.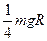 |
B.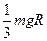 |
C.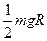 |
D.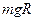 |
如图所示,小球A从半径为R=0.8 m的1/4光滑圆弧轨道的上端点以v0=3 m/s的初速度开始滑下,到达光滑水平面上以后,与静止于该水平面上的钢块B发生碰撞,碰撞后小球A被反向弹回,沿原路进入轨道运动恰能上升到它下滑时的出发点(此时速度为零).设A、B碰撞机械能不损失,g取10 m/s2,求:
(1)小球A刚滑上水平面的速度.
(2)A和B的质量之比.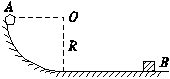
如图所示,一个小环沿竖直放置的光滑圆环形轨道做圆周运动.小环从最高点A滑到最低点B的过程中,小环线速度大小的平方 随下落高度h的变化图象可能是图中的( )
随下落高度h的变化图象可能是图中的( )
如图所示,滑块质量为m,与水平地面的动摩擦因数为0.1,它获得一大小为3 的水平速度后,由A向B滑行5R,并滑上光滑的半径为R的
的水平速度后,由A向B滑行5R,并滑上光滑的半径为R的 圆弧BC,在C点的正上方有一离C高度也为R的旋转平台,沿平台直径方向开有两个离轴心距离相等的小孔P、Q,旋转时两孔均能达到C点的正上方,若滑块过C点后穿过P,又恰能从Q孔落下,则平台的角速度ω应满足什么条件?
圆弧BC,在C点的正上方有一离C高度也为R的旋转平台,沿平台直径方向开有两个离轴心距离相等的小孔P、Q,旋转时两孔均能达到C点的正上方,若滑块过C点后穿过P,又恰能从Q孔落下,则平台的角速度ω应满足什么条件?

A、B两个小物块用轻绳连结,绳跨过位于倾角为300的光滑斜面顶端的轻滑轮,滑轮与转轴之间的摩擦不计,斜面固定在水平桌面上,如图甲所示.第一次, A悬空,B放在斜面上,用t表示B自斜面底端由静止开始运动至斜面顶端所需的时间.第二次,将A和B位置互换,使B悬空,A放在斜面上,发现A自斜面底端由静止开始运动至斜面顶端所需的时间为t/2.(重力加速度g已知)
(1)求A与B两小物块的质量之比.
(2)若将光滑斜面换成一个半径为R(已知)的半圆形光滑轨道固定在水平桌面上,将这两个小物块用轻绳连结后,如图放置,现将B球从轨道边缘由静止释放.若不计一切摩擦,求:B沿半圆形光滑轨道滑到底端时,A、B的速度大小.


倾斜雪道的长为25 m,顶端高为15 m,下端经过一小段圆弧过渡后与很长的水平雪道相接,如图所示。一滑雪运动员在倾斜雪道的顶端以水平速度v0=8 m/s飞出,在落到倾斜雪道上时,运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度而不弹起。除缓冲外运动员可视为质点,过渡轨道光滑,其长度可忽略。设滑雪板与雪道的动摩擦因数μ=0.2,求运动员在水平雪道上滑行的距离(取g=10 m/s2)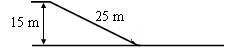
试题篮
()