如图所示,QB段为一半径为 的光滑圆弧轨道,AQ段为一长度为
的光滑圆弧轨道,AQ段为一长度为 的粗糙水平轨道,两轨道相切于Q点,Q在圆心O的正下方,整个轨道位于同一竖直平面内。物块
的粗糙水平轨道,两轨道相切于Q点,Q在圆心O的正下方,整个轨道位于同一竖直平面内。物块 的质量为m=1kg(可视为质点),P与AQ间的动摩擦因数
的质量为m=1kg(可视为质点),P与AQ间的动摩擦因数 ,若物块
,若物块 以速度v0从A点滑上水平轨道,到C点后又返回A点时恰好静止。(取
以速度v0从A点滑上水平轨道,到C点后又返回A点时恰好静止。(取 )求:
)求:
(1)v0的大小;
(2)物块P第一次刚通过Q点时对圆弧轨道的压力。
如图所示,质量M=2 kg的滑块套在光滑的水平轨道上,质量m=1 kg的小球通过长L=0.5 m的轻质细杆与滑块上的光滑轴O连接,小球和轻杆可在竖直平面内绕O轴自由转动,开始轻杆处于水平状态,现给小球一个竖直向上的初速度v0=4 m/s,g取10 m/s2。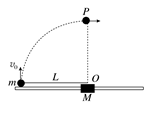
(1)若锁定滑块,试求小球通过最高点P时对轻杆的作用力大小和方向;
(2)解除对滑块的锁定,小球过最高点时速度大小v′=2 m/s,求此时滑块的速度大小。
(10分)在2008年北京残奥会开幕式上,运动员手拉绳索向上攀登,最终点燃了主火炬,体现了残疾运动员坚忍不拔的意志和自强不息的精神。为了探究上升过程中运动员与绳索和吊椅间的作用,可将过程简化。一根不可伸缩的轻绳跨过轻质的定滑轮,一端挂一吊椅,另一端被坐在吊椅上的运动员拉住,如图所示。设运动员的质量为65kg,吊椅的质量为15kg,不计定滑轮与绳子间的摩擦。重力加速度取g=10m/s2。当运动员与吊椅一起正以加速度a=1m/s2上升时,试求: 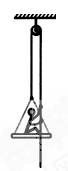
(1)运动员竖直向下拉绳的力;
(2)运动员对吊椅的压力。
如图所示,小球被轻质细绳系住斜吊着放在光滑斜面上,小球与斜面均处于静止状态,设小球质量m=2 kg,斜面倾角α=30°,细绳与竖直方向夹角θ=30°,光滑斜面体的质量M=3 kg,置于粗糙水平面上.(g取10 m/s2)求: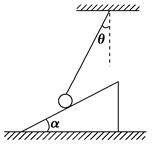
(1)细绳对小球拉力的大小;
(2)地面对斜面体的摩擦力的大小和方向.
如图所示,固定在水平面上的斜面其倾角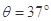 ,长方形木块A的MN面上钉着一颗钉子,质量m=1.5kg的小球B通过一细线与小钉子相连接,细线与斜面垂直。木块与斜面间的动摩擦因数
,长方形木块A的MN面上钉着一颗钉子,质量m=1.5kg的小球B通过一细线与小钉子相连接,细线与斜面垂直。木块与斜面间的动摩擦因数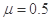 。现将木块由静止释放,木块与小球将一起沿斜面下滑。求在木块下滑的过程中;(取g=l0m/s2)
。现将木块由静止释放,木块与小球将一起沿斜面下滑。求在木块下滑的过程中;(取g=l0m/s2)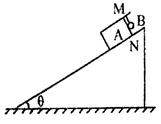
(1)木块与小球的共同加速度的大小;
(2)小球对木块MN面的压力的大小和方向。
游乐园的小型“摩天轮”上对称站着质量均为m的8位同学,如图所示,“摩天轮”在竖直平面内逆时针匀速转动,若某时刻转到顶点a上的甲同学让一小重物做自由落体运动,并立即通知下面的同学接住,结果重物掉落时正处在c处(如图)的乙同学恰好在第一次到达最低点b处接到,己知“摩天轮”半径为R,重力加速度为g,(不计人和吊篮的大小及重物的质量).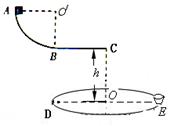
问:(1)接住前重物下落运动的时间t="?" (2)人和吊篮随“摩天轮”运动的线速度大小v=? (3)乙同学在最低点处对地板的压力FN=?
如图所示,竖直固定放置的粗糙斜面AB的下端与光滑的圆弧BCD的B点相切,圆弧轨道的半径为R,圆心O与A、D在同一水平面上,∠COB=θ.现有质量为m的小物体从距D点为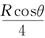 的高处无初速释放,已知物体恰能从D点进入圆轨道,求:
的高处无初速释放,已知物体恰能从D点进入圆轨道,求: 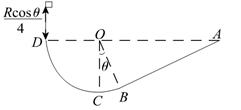
(1)为使小物体不会从A点冲出斜面,小物体与斜面间的动摩擦因数至少为多少?
(2)若小物块与斜面间的动摩擦因数μ=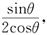 则小物体在斜面上通过的总路程为多少?
则小物体在斜面上通过的总路程为多少?
(3)在(2)的条件下,当小物体通过圆弧轨道最低点C时,对C的最大压力和最小压力各是多少?
(15分)如图,一不可伸长的轻绳上端悬挂于O点,下端系一质量m=1.0kg的小球。现将小球拉到A点(保持绳绷直)由静止释放,当它经过B点时绳恰好被拉断,小球平抛后落在水平地面上的C点。地面上的D点与OB在同一竖直线上,已知绳长L=1.0m,B点离地高度H=1.0m,A、B两点的高度差h=0.5m,重力加速度g取10m/s2,不计空气阻力影响,求: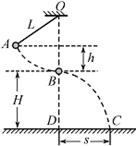
⑴地面上DC两点间的距离s;⑵轻绳所受的最大拉力大小。
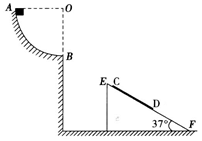
如图所示,AB段为一半径R=0.2m的光滑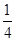 圆弧轨道,EF为一倾角是37°的足够长的光滑固定斜面,斜面上有一质量为0.1kg的薄木板CD,开始时木板被锁定.一质量也为0.1kg的物块从A点由静止开始下滑,通过B点后水平抛出,经过一段时间后恰好以平行于木板的方向滑上木板,在物块滑上木板的同时,木板解除锁定,下滑过程中某时刻物块和木板能达到共同速度.已知物块与木板间的动摩擦因数为
圆弧轨道,EF为一倾角是37°的足够长的光滑固定斜面,斜面上有一质量为0.1kg的薄木板CD,开始时木板被锁定.一质量也为0.1kg的物块从A点由静止开始下滑,通过B点后水平抛出,经过一段时间后恰好以平行于木板的方向滑上木板,在物块滑上木板的同时,木板解除锁定,下滑过程中某时刻物块和木板能达到共同速度.已知物块与木板间的动摩擦因数为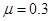 (g取
(g取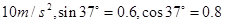 ),
),
求:(1)物块到达B点时对圆弧轨道压力的大小;
(2)物块做平抛运动的时间;
(3)若下滑过程中某时刻物块和木板达到共同速度,则这个速度为多大?(木板足够长)
根据玻尔理论,电子绕氢原子核运动可以看作是仅在库仑引力作用下的匀速圆周运动,已知电子的电荷量为e,质量为m,电子在第1轨道运动的半径为r1,静电力常量为k。
(1)电子绕氢原子核做圆周运动时,可等效为环形电流,试计算电子绕氢原子核在第1轨道上做圆周运动的周期及形成的等效电流的大小;
(2)氢原子在不同的能量状态,对应着电子在不同的轨道上绕核做匀速圆周运动,电子做圆周运动的轨道半径满足rn=n2r1,其中n为量子数,即轨道序号,rn为电子处于第n轨道时的轨道半径。电子在第n轨道运动时氢原子的能量En为电子动能与“电子-原子核”这个系统电势能的总和。理论证明,系统的电势能Ep和电子绕氢原子核做圆周运动的半径r存在关系:Ep=-k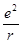 (以无穷远为电势能零点)。请根据以上条件完成下面的问题。
(以无穷远为电势能零点)。请根据以上条件完成下面的问题。
①试证明电子在第n轨道运动时氢原子的能量En和电子在第1轨道运动时氢原子的能量E1满足关系式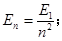
②假设氢原子甲核外做圆周运动的电子从第2轨道跃迁到第1轨道的过程中所释放的能量,恰好被量子数n=4的氢原子乙吸收并使其电离,即其核外在第4轨道做圆周运动的电子脱离氢原子核的作用范围。不考虑电离前后原子核的动能改变,试求氢原子乙电离后电子的动能。
半径R=0.50 m的光滑圆环固定在竖直平面内,轻质弹簧的一端固定在环的最高点A处,另一端系一个质量m=0.20 kg的小球,小球套在圆环上,已知弹簧的原长为L0=0.50 m,劲度系数k=5N/m,将小球从如图所示的位置由静止开始释放,小球将沿圆环滑动并通过最低点C,在C点时速度vC=3m/s,g取10 m/s2.求: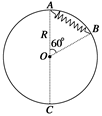
(1)小球经过C点时的弹簧的弹性势能的大小;
(2)小球经过C点时对环的作用力的大小和方向.
如图所示,在质量为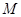 的电动机上,装有质量为
的电动机上,装有质量为 的偏心轮,偏心轮的重心
的偏心轮,偏心轮的重心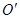 距转轴的距离为
距转轴的距离为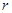 .当偏心轮重心在转轴
.当偏心轮重心在转轴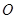 正上方时,电动机对地面的压力刚好为零.求电动机转动的角速度
正上方时,电动机对地面的压力刚好为零.求电动机转动的角速度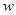 .
.
试题篮
()