两个宽度为D、质量为m的相同的小物块A、B,一带孔圆环C的质量为2m,半径为d,它们的厚度均可忽略。一不可伸长的轻质细绳绕过光滑的定滑轮,一端连接A物块,一端穿过圆环C的小孔连接B物块,如图所示。现将A置于水平地面,距滑轮底端3L,BC距水平地面为L,在BC的正下方有一深 、宽
、宽 的凹槽。B、C落地后都不再弹起。通过具体的计算分析,画出A物块在上升过程中的速度—时间(v-t)图象。
的凹槽。B、C落地后都不再弹起。通过具体的计算分析,画出A物块在上升过程中的速度—时间(v-t)图象。

如图所示,质量分别是m1、m2的两个木块,用轻质细线相连,在水平外力F的作用下在粗糙的水平地面上向右做匀速直线运动,某时刻剪断细线,在A停止运动以前,对于A、B系统的总动能下列说法中正确的是:( ) 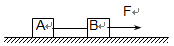
A.不变 B.减小 C.增加 D.先增加后减小
如图所示,左侧是倾角为60°的斜面、右侧是 圆弧面的物体固定在水平地面上,圆弧面底端切线水平,一根两端分别用轻绳系有质量为m1、m2的小球跨过其顶点上的小滑轮。当它们处于平衡状态时,连结m2小球的轻绳与水平线的夹角为600,不计一切摩擦,两小球可视为质点。两小球的质量之比ml : m2等于( )
圆弧面的物体固定在水平地面上,圆弧面底端切线水平,一根两端分别用轻绳系有质量为m1、m2的小球跨过其顶点上的小滑轮。当它们处于平衡状态时,连结m2小球的轻绳与水平线的夹角为600,不计一切摩擦,两小球可视为质点。两小球的质量之比ml : m2等于( )
| A.1 : l | B.2 : 3 | C.3 : 2 | D.3 : 4 |
在2008年北京残奥会开幕式上,运动员手拉绳索向上攀登,最终点燃了主火炬,体现了残疾运动员坚忍不拔的意志和自强不息的精神。为了探求上升过程中运动员与绳索和吊椅间的作用,可将过程简化。一根不可伸缩的轻绳跨过轻质的定滑轮,一端挂一吊椅,另一端被坐在吊椅上的运动员拉住,如图所示。设运动员的质量为65kg,吊椅的质量为15kg,不计定滑轮与绳子间的摩擦,重力加速度取g=10m/s2。当运动员与吊椅一起正以加速度a=1m/s2上升时,试求:⑴运动员受到竖直绳的拉力大小 N;⑵运动员对吊椅的压力大小 N。
建筑工人用如图所示的定滑轮装置运送建筑材料。质量为70kg的工人站在地面上,通过定滑轮将20kg的建筑材料以0.5 m/s2的加速度拉升,忽略绳子和定滑轮的质量及定滑轮的摩擦,则工人对地面的压力大小为(g=10m/s2) ( )
| A.510 N | B.490 N |
| C.890 N | D.910 N |
(8分)如图所示,水平面上有一固定着轻质定滑轮O的木块A,它的上表面与水平面平行,它的右侧是一个倾角θ=370的斜面。放置在A上的物体B和物体C通过一轻质细绳相连,细绳的一部分与水平面平行,另一部分与斜面平行。现对A施加一水平向右的恒力F.使A、B、C恰好保持相对静止。已知A、B、C的质量均为m,重力加速度为g,不计一切摩擦,求恒力F的大小。(sin370=0.6,cos370=0.8)
一个单摆悬挂在小车上,随小车沿着斜面滑下,图中的虚线①与斜面垂直,虚线②沿斜面方向,则可判断出 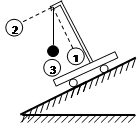
| A.如果斜面光滑,摆线与②重合 |
| B.如果斜面光滑,摆线与①重合 |
| C.如果斜面粗糙但摩擦力小于下滑力,摆线位于②与③之间 |
| D.如果斜面粗糙但摩擦力大于下滑力,摆线位于②与③之间 |
如图所示,物块A、B质量分别为mA=0.8kg,mB=0.3kg,A、B与地面摩擦因素均为0.2,滑轮绳子质量及摩擦均不计。外力F=4N作用于A上,A、B的加速度分别为:
A.2.4m/s2,1.6m/s2 B.0.6m/s2,1.2m/s2
C.2.4m/s2,0.6m/s2 D.1.2m/s2,0.6m/s2
在静止的电梯里放一桶水,把一个轻弹簧的一端连在桶底,另一端连接在浸没在水中的质量为m的软木塞上,轻弹簧处于伸长状态,如图所示.当电梯由静止开始匀加速下降(a<g)时,轻弹簧的长度将发生怎样的变化:( )
| A.伸长量保持不变 | B.由伸长变为压缩   |
C.伸长量增加 | D.伸长量减小 |

如图所示,两木块的质量M是m的二倍,水平面光滑,当用水平力F分别推m和M时,两物体之间弹力之比N1:N2应为:
| A.1:1 | B.1:2 | C.2:1 | D.3:1 |
如图所示,mA=4.Okg,mB=2.Okg,A和B紧靠着放在光滑水平面上,从t=O时刻起,对B施加向右的水平恒力F2=4.ON,同时对A施加向右的水平变力F1,F1变化规律如图所示。下列相关说法中正确的是

A.当t=0时,A、B物体加速度分别为aA=5m/s2,aB=2m/s2
B.A物体作加速度减小的加速运动,B物体作匀加速运动
C.t="12" s时刻A、B将分离,分离时加速度均为a=2m/s2
D.A、B分离前后,A物体加速度变化规律相同
如图所示,质量分别为mA、mB的A、B两物块用轻线连接放在倾角为θ的斜面上,用始终平行于斜面向上的恒力F拉A,使它们沿斜面匀加速上升,A、B与斜面的动摩擦因数均为μ,为了增加轻线上的张力,可行的办法是
A.增大A物的质量 B.增大B物的质量
C.增大倾角θ D.增大动摩擦因数μ
如图所示,质量为m的小物块静止地放在半径为R的半球体上,物块与半球体间的动摩擦因数为μ,物块与球心的连线与水平地面的夹角为θ,下列说法中正确的是
| A.地面对半球体的摩擦力方向水平向左 |
| B.物块对半球体的压力大小为mgcosθ |
| C.物块所受摩擦力大小为μmgcosθ |
| D.物块所受摩擦力大小为mgcosθ |
物体A、B质量分别为mA=2kg、mB=3kg,二者间用牢固的细线连接,现对A物体施以竖直向上的恒力F的作用,F=60N,使A、B两物体共同向上做匀加速运动。取g="10" m/s2,关于细线中张力T的大小,以下说法正确的是
A.T大小为20N
B.T大小为30N
C.T大小为36N
D.T大小为60N
如图,一块质量为M = 2kg,长L = 1m的匀质木板放在足够长的光 滑水平桌面上,初始时速度为零.板的最左端放置一个质量m = 1kg的小物块,小物块与木板间的动摩擦因数为μ = 0.2,小物块上连接一根足够长的水平轻质细绳,细绳跨过位于桌面边缘的定滑轮(细绳与滑轮间的摩擦不计,木板与滑轮之间距离足够长,g = 10m/s2)。
滑水平桌面上,初始时速度为零.板的最左端放置一个质量m = 1kg的小物块,小物块与木板间的动摩擦因数为μ = 0.2,小物块上连接一根足够长的水平轻质细绳,细绳跨过位于桌面边缘的定滑轮(细绳与滑轮间的摩擦不计,木板与滑轮之间距离足够长,g = 10m/s2)。
⑴若木板被固定,某人以恒力F = 4N向下拉绳,则小木块滑离木板所需要的时间是多少?
⑵若木板不固定,某人仍以恒力F = 4N向下拉绳,则小木块滑离木板所需要的时间是多少?
⑶若人以恒定速度v1=1m/s向下匀速拉绳,同时给木板一个v2 = 0.5m/s水平向左的初速度,则木块滑离木板所用的时间又是多少?
试题篮
()