如图所示,两平行金属板A、B板长L=8cm,两板间距离d=8cm,A板比B板电势高300V,一带正电的粒子电量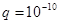 C,质量
C,质量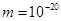 kg,沿两板中线垂直电场线飞入电场,初速度
kg,沿两板中线垂直电场线飞入电场,初速度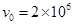 m/s,粒子飞出平行板电场后经过界面MN、PS间的无电场区域后,进入PS的右侧,已知两界面MN、PS相距为
m/s,粒子飞出平行板电场后经过界面MN、PS间的无电场区域后,进入PS的右侧,已知两界面MN、PS相距为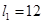 cm.在界面PS右侧与A板在同一水平线上放置荧光屏bc.(粒子所受重力不计)
cm.在界面PS右侧与A板在同一水平线上放置荧光屏bc.(粒子所受重力不计)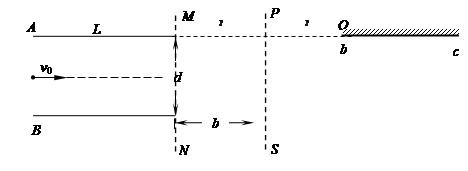
(1)求粒子飞出平行金属板时速度的大小和方向;
(2)求出粒子经过界面PS时离P点的距离h为多少;
(3)若PS右侧与A板在同一水平线上距离界面PS为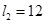 cm的O点固定一点电荷
cm的O点固定一点电荷 C,(图中未画出,设界面PS右边点电荷的电场分布不受界面等影响,界面PS左边不存在点电荷的电场),试求粒子穿过界面PS后打在荧光屏bc的位置离O点的距离为多少?(静电力常数
C,(图中未画出,设界面PS右边点电荷的电场分布不受界面等影响,界面PS左边不存在点电荷的电场),试求粒子穿过界面PS后打在荧光屏bc的位置离O点的距离为多少?(静电力常数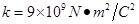 ,
,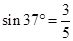
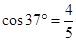 )
)
如图21所示,一根长0.1m的细线,一端系着一个质量为0.18kg的小球,拉住线的另一端,使球在光滑的水平桌面上作匀速圆周运动,使小球的转速很缓慢地增加,当小球的转速增加到开始时转速的3倍时,细线断开,线断开前的瞬间线的拉力比开始时大40N,求:
(1)线断开前的瞬间,线的拉力大小。
(2)线断开的瞬间,小球运动的线速度。
(3)如果小球离开桌面时,速度方向与桌边的夹角为 ,桌面高出地面0.8m,求小球飞出后的落地点距桌边的水平距离。
,桌面高出地面0.8m,求小球飞出后的落地点距桌边的水平距离。
一个质量为m的小球拴在钢绳的一端,另一端施加大小为F1的拉力作用,在水平面上做半径为R1的匀速圆周运动。今将力的大小改变为F2,使小球仍在水平面上做匀速圆周运动,但半径变为R2,小球运动的半径由R1变为R2过程中拉力对小球做的功。
“太极球”是近年来在广大市民中较流行的一种健身器材.做该项运动时,健身者半马步站立,手持太极球拍,拍上放一橡胶太极球,健身者舞动球拍时,球却不会掉落地上.现将太极球简化成如题图所示的平板和小球,熟练的健身者让球在竖直面内始终不脱离板而做匀速圆周运动,且在运动到图中的A、B、C、D位置时球与板间无相对运动趋势.A为圆周的最高点,C为最低点,B、D与圆心O等高.若球恰能到达最高点,设球的重力为1N.求:
(1)平板在C处对球施加力的大小?
(2)当球运动到B位置时,平板与水平方向的夹角θ为多大?
如图所示是一个水平转盘的示意图,盘上距转轴0.5m处有一质量为0.5kg的零件随转盘做匀速圆周运动.求:
(1)如果零件在转盘上无滑动,请画出零件的受力示意图.
(2)如果零件与转盘之间的最大静摩擦力为1.96N ,零件随转盘转动时,转盘的转速最大不能大于多少?
用长为L的细绳栓住一个质量为m的小球,如图所示,当小球在水平面内做匀速圆周运动时,细绳与竖直方向成 角,求小球做匀速圆周运动的周期及细绳对小球的拉力。
角,求小球做匀速圆周运动的周期及细绳对小球的拉力。
2010年温哥华冬奥会双人滑比赛中,申雪、赵宏博拿到中国花样滑冰史上首枚冬奥会金牌,如图所示,赵宏博(男)以自己为转轴拉着申雪(女)做匀速圆周运动,转速为30r/min.申雪的脚到转轴的距离为1.6m.求:
(1)申雪做匀速圆周运动的角速度;
(2)申雪的脚运动速度的大小.
如图所示,有界匀强磁场的磁感应强度为B特斯拉,磁场方向垂直于纸面向里,MN是磁场的左边界.在磁场中A处放一个放射源内装 Ra(镭),
Ra(镭), Ra放出某种射线后衰变成
Ra放出某种射线后衰变成 Rn(氡),粒子可向各个方向射出.若A距磁场的左边界MN的距离OA="d" 时,从A点沿垂直OA向上射出的质量较小粒子,恰好使放在MN左侧的粒子接收器接收到垂直于边界MN方向射出的该粒子,此时接收器位置距OA直线的距离也为d.由此可以推断出(取原子质量单位用m0表示,电子电量用e表示).
Rn(氡),粒子可向各个方向射出.若A距磁场的左边界MN的距离OA="d" 时,从A点沿垂直OA向上射出的质量较小粒子,恰好使放在MN左侧的粒子接收器接收到垂直于边界MN方向射出的该粒子,此时接收器位置距OA直线的距离也为d.由此可以推断出(取原子质量单位用m0表示,电子电量用e表示).
试写出 Ra衰变的方程且确定射出的质量较小的粒子在磁场中的轨迹圆半径是多少?
Ra衰变的方程且确定射出的质量较小的粒子在磁场中的轨迹圆半径是多少?
射出的质量较小的粒子的速度为多少?
这一个静止镭核 Ra衰变时亏损质量多大?
Ra衰变时亏损质量多大?
(提示:动量守恒定律在微观领域仍适用,系统增加机械能来自核能释放)
一物体在水平面内沿半径 R=" 0.20" m的圆形轨道做匀速圆周运动,线速度V=0.2m/s,试求:(1)它的向心加速度为多少m/s2?(2)它的角速度为多少 rad/s?
如图所示,AB为竖直转轴,细绳AC和BC的结点C系一质量为m的小球,两绳能承担的最大拉力均为2mg。当AC和BC均拉直时∠ABC=90°,∠ACB=53°,BC=1m。竖直轴AB匀速转动,C球在水平面内做匀速圆周运动。
求:
(1)要使两条细绳都拉直,C球的线速度至少多大?
(2)当C球的线速度增大时,AC和BC哪条绳先断?当其中一条绳刚要断时,C球的线速度多大?
(g=10m/s2,sin53°=0.8,cos53°=0.6)
如图所示,在半径为R,质量分布均匀的某星球表面,有一倾角为θ的斜坡。以初速度v0向斜坡水平抛出一个小球。测得经过时间t,小球垂直落在斜坡上的C点。求:(1)小球落在斜坡上时的速度大小v;(2)该星球表面的重力加速度g;(3)卫星绕该星球表面做匀速圆周运动的速度v′。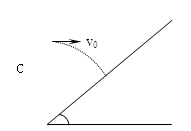
如图,长为L的不可伸长的细线,拴一质量为m的小球,一端固定于O点,让其在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图所示。当摆线L与竖直方向的夹角是α时,求:
(1)线的拉力F;
(2)小球运动的周期。
如图所示,在光滑的圆锥体顶端用长为L的细线悬挂一质量为m的小球。圆锥体固定在水平面上不动,其轴线沿竖直方向,母线与轴线之间的夹角θ=300。现使小球以一定的速率绕圆锥体的轴线在水平面内做圆周运动.
(1)当小球速率 时,求细线对小球的拉力;
时,求细线对小球的拉力;
(2)当小球速率 时,求细线对小球的拉力。
时,求细线对小球的拉力。
某研究性学习小组首先根据小孔成像原理估测太阳半径,再利用万有引力定律估算太阳的密度.准备的器材有:①不透光圆筒,一端封上不透光的厚纸,其中心扎一小孔,另一端封上透光的薄纸;②毫米刻度尺.已知地球绕太阳公转的周期为T,万有引力常量为G.要求:(1)简述根据小孔成像原理估测太阳半径R的过程.(2)利用万有引力定律推算太阳密度.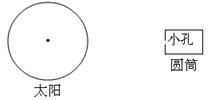
家用台式计算机的硬盘磁道和扇区如图所示,数据区域的内半径为R1=1.0 cm,外半径为R2=5.0 cm,径向磁道密度为N=600条/mm,(即每条磁道是不同半径的同心圆),每个磁道分成a=8192个扇区(每扇区为 圆周),每个扇区可以记录512个字节。电动机使磁盘以7200r/min的转速匀速转动。
圆周),每个扇区可以记录512个字节。电动机使磁盘以7200r/min的转速匀速转动。
求:(1)假设磁头在读、写数据时是不动的,磁盘每转一圈,磁头沿半径方向跳动一个磁道。则不计磁头在磁道间移动的时间,求计算机1s内最多可以从一个磁盘面上读取多少个字节?
(2)假设磁盘每转一圈,磁头沿径向向外移动一条磁道,已知每条磁道宽度均匀,并且磁头相对于磁盘以恒定的线速度v=3.14 m/s运动.求将一张磁盘全部读完一遍所用时间是多少?
m/s运动.求将一张磁盘全部读完一遍所用时间是多少?
(以上结果均保留3为有效数字)
试题篮
()