如图所示,有一内壁光滑的试管装有质量为1 g的小球,试管的开口端封闭后安装在水平轴O上,转动轴到管底小球的距离为5 cm,让试管在竖直平面内做匀速转动。问:
(1)转动轴达某一转速时,试管底部受到小球的压力的最大值为最小值的3倍,此时角速度多大?
(2)当转速ω=10 rad/s时,管底对小球的作用力的最大值和最小值各是多少?(g取10 m/s2)
在绕地球作匀速圆周运动的太空仓内,按照同学们使用的新人教版教材要求,能完成的实验是:
| A.验证力的平行四边形法则 |
| B.探究弹簧形变量与弹力的关系 |
| C.探究物体加速度与质量和合外力的关系 |
| D.用平抛运动测初速度 |
甲、乙两物体都做匀速圆周运动,其质量之比为1:2,转动半径之比为1:2,在相等时间里甲转过30°,乙转过45°,则它们所受外力的合力之比为 ( )
| A.1:4 | B.1:6 | C.9:16 | D.1:9 |
如图所示,三段细线长OA=AB=BC, A、B、C三球质量相等,当它们绕O点在光滑的水平桌面上以相同的角速度作匀速圆周运动时,则三段线的拉力TOA:TAB:TBC为( )
A.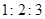 B.
B.
C.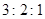 D.
D.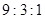
“飞车走壁”杂技表演简化后的模型如图所示,表演者沿表演台的侧壁做匀速圆周运动。若表演时杂技演员和摩托车的总质量不变,摩托车与侧壁间沿侧壁倾斜方向的摩擦力恰好为零,轨道平面离地面的高度为H,侧壁倾斜角度α不变,则下列说法中正确的是( ) 
| A.摩托车做圆周运动的H越高,角速度越小 |
| B.摩托车做圆周运动的H越高,线速度越小 |
| C.摩托车做圆周运动的H越高,向心力越大 |
| D.摩托车对侧壁的压力随高度H变大而减小 |
质量为m的物体沿半径为R的半球形金属球壳滑到最低点时的速度大小为v,如右图所示,若物体与球壳间的动摩擦因数为μ,则物体在最低点时 ( )
A.向心加速度为
B.向心力为
c.摩擦力为
D.对球壳的压力为
一半径为R的雨伞绕柄以角速度 匀速旋转,如右图所示,伞边缘距地面高h,甩出的水滴在地面上形成一个半径为r的圆,则角速度的表达式为( )
匀速旋转,如右图所示,伞边缘距地面高h,甩出的水滴在地面上形成一个半径为r的圆,则角速度的表达式为( )
A. |
B. |
C. |
D. |
球A和球B可在光滑杆上无摩擦滑动,两球用一根细绳连接如右图所示,球A的质量是球B的两倍,当杆以角速度ω匀速转动时,两球刚好保持与杆无相对滑动,那么 ( )
| A.球A受到的向心力大于B受到的向心力 |
| B.球A转动的半径是球B转动半径的一半 |
| C.当A球质量增大时,球A向外运动 |
| D.当ω增大时,球B向外运动 |
如图所示,A.B两个小球,质量相等,用一根轻绳相连,另有一根轻绳的两端分别连接O点和B球,让两小球绕O点在光滑水平桌面上以相同的角速度做匀速圆周运动,若OB绳上的拉力为F1,AB绳上的拉力为F2,OB=2AB,则 ( )
A.F1:F2=2:3 B.F1:F2=3:2 C.F1:F2=5:3 D.F1:F2=2:1
水平面上有倾角为θ、质量为M的斜面体,质量为m的小物块放在斜面上,现用一平行于斜面、大小恒定的拉力F作用于小物块上,绕小物块旋转一周,这个过程中斜面体和木块始终保持静止状态。下列说法中正确的是
| A.小物块受到斜面的最大摩擦力为F+mgsinθ |
| B.小物块受到斜面的最大摩擦力为F- mgsinθ |
| C.斜面体受到地面的最大摩擦力为F |
| D.斜面体受到地面的最大摩擦力为Fcosθ |
如图所示,长为R的轻质杆(质量不计),一端系一质量为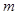 的小球(球大小不计),绕杆的另一端O在竖直平面内做匀速圆周运动,若小球最低点时,杆对球的拉力大小为1.5
的小球(球大小不计),绕杆的另一端O在竖直平面内做匀速圆周运动,若小球最低点时,杆对球的拉力大小为1.5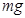 ,求:
,求:
①小球最低点时的线速度大小?
②小球通过最高点时,杆对球的作用力的大小及方向?
③小球以多大的线速度运动,通过最高处时杆对球不施力?
关于圆周运动,下列说法正确的是
| A.匀速圆周运动是匀速运动 |
| B.匀速圆周运动是变速运动 |
| C.匀速圆周运动是变加速运动 |
| D.做圆周运动的物体加速度一定始终指向圆心 |
下列关于离心现象的说法正确的是:
| A.当物体所受的离心力大于向心力时产生离心现象 |
| B.做匀速圆周运动的物体,当它所受的一切力都突然消失时,它将做背离圆心的圆周运动 |
| C.做匀速圆周运动的物体,当它所受的一切力都突然消失时它将沿切线做直线运动 |
| D.做匀速圆周运动的物体,当它所受的一切力都突然消失时它将做曲线运动 |
试题篮
()